🌈以下是自己关于锁相环的学习及认识，参考教材是杜勇老师主编的《锁相环原理及FPGA实现》，老师的教材编写风格真的很幽默，而且通俗易懂，虽然很难，但是不乏趣味性。参考教材下载链接已放在文末。

一. 锁相环的组成

1.1 总体概述

 根据不同的应用情况，实际工程设计中的锁相环路有很多种，如用于载波提取的窄带跟踪电路、用于解调器的解调环、用于提高本振频率稳定度的分频或倍频锁相环电路等。虽然存在各种形式的环路，但它们都是由三个基本部件组成：鉴相器（Phase Detector，PD）、环路滤波器（Loop Filter，LF）和电压控制振荡器（Voltage ControlledOscillator，VCO）。其基本电路组成原理图如下：


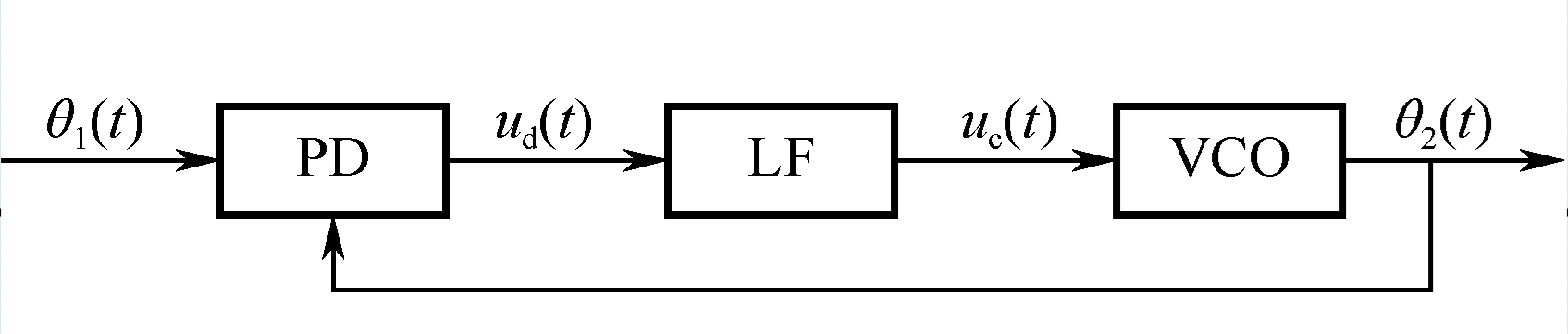
1711425983219.png

 为便于后续对环路模型的深入讨论，首先有必要对图 中各节点信号之间的转换关系进行明确。其中$\theta_{1}(t)$为输入信号的瞬时相位，以弧度（ rad）为单位；$\theta_{2}(t)$ 为 VCO 输出频率 信 号 的 瞬时 相 位 ， 以弧 度 （ rad ） 为 单 位 ； $u_{d}(t)$ 为 $\theta_{1}(t)$与 $\theta_{2}(t)$ 的 差 值 $\theta_{e}(t)$（ 令$\theta_\mathrm{e}(t)=\theta_1(t)-\theta_2(t)$）的函数，是一个电压信号，单位为伏特（ V）； $u_{c}(t)$ 为 $u_{d}(t)$ 经 LF 滤波后的电压信号，单位为伏特（ V）。

1.2 压控振荡器VCO

  1. 从 VCO 的功能来看，它是一个电压与频率的变换装置，在环路中作为压控振荡器，它的振荡频率随输入控制电压线性地变化，其变化关系为$$\omega_\mathrm{v}(t)=\omega_\mathrm{o}+K_0u_\mathrm{c}(t)$$

    式中，$w_{v}(t)$是压控振荡器的瞬时角频率，单位为 rad/s ； $w_{0}$ 是压控振荡器的固有振荡角频率，即没有输入控制电压情况下的振荡角频率，单位为 rad/s ； $K_{0}$ 为 VCO 的频率控制灵敏度或称增益系数，单位是 rad/(s*V) 。实际应用中，模拟压控振荡器的控制特性只有有限的线性控制范围，超出这个范围之后控制灵敏度将会下降。

  2. 使用SystemView对VCO器件进行仿真

    1712629239948.png

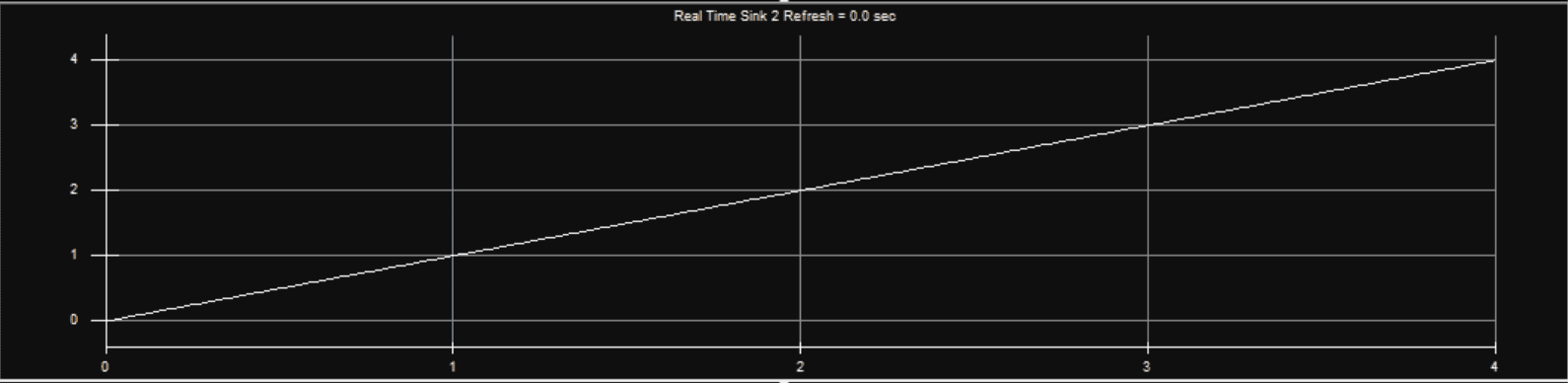
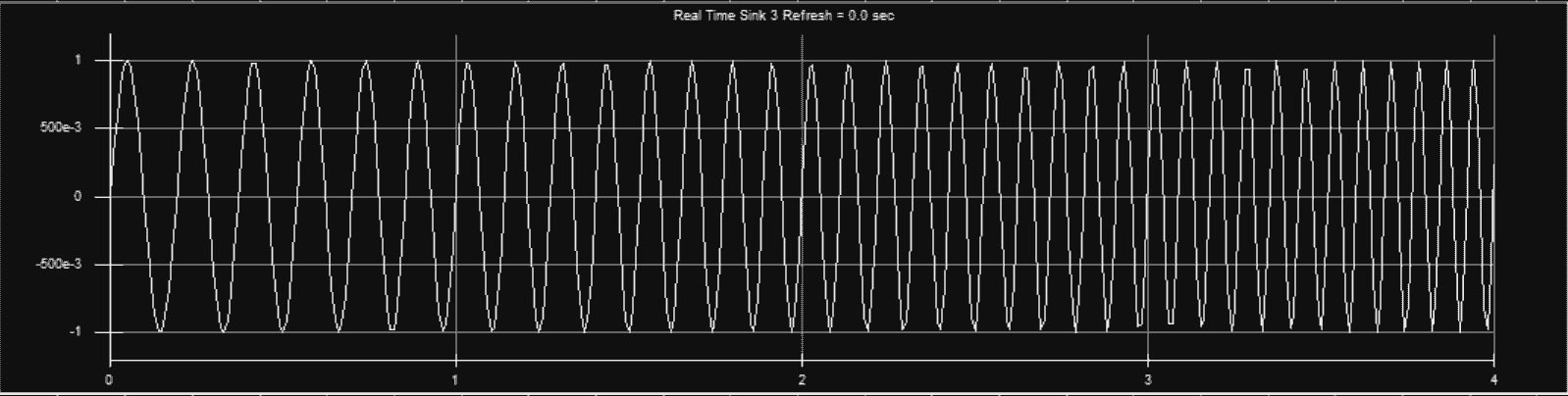
    元件名称 元件参数（Parameters）
    信号源 Source: Time Gain= 1v/sec Offset = 0v
    VCO Amp= 1v Freq: 5Hz Phase= 0deg Mod_Gain= 2Hz/v Output_0=Quadrature (Sin0)

    1712629383883.png

    1712629493586.png

    根据最后的仿真波形不难得出，随着输入电压的增大，VCO的输出信号频率也随之增大。

  3. VCO是一个积分器

     因为对信号瞬时相位进行微分，就可以得到信号的瞬时频率；反之，对信号的频率进行积分，就可以得到信号的瞬时相位。因此VCO 输入电压$u_{c}(t)$与输出信号的相位之间的关系如下：$$\int_0^t\omega_\mathrm{v}(\tau)\mathrm{d}\tau=\omega_\mathrm{o}t+K_0\int_0^tu_\mathrm{c}(\tau)\mathrm{d}\tau $$

    上式中除了积分因子之外，还有线性乘法因子，所以它还不是纯粹的积分器。由于鉴相器的输出$u_{d}(t)$，为$\theta_{1}(t)$ 与 $\theta_{2}(t)$的差值 $\theta_{e}(t)$的函数。也就是说，$u_{d}(t)$不是与 VCO 的瞬时相位相关，而是与 VCO 和输入信号的瞬时相位差相关的。既然是相位差，因此完全可以人为任意设定一个基准相位（即参考相位），输入信号与输出信号的相位都与这个基准相位进行比较，再将比较的结果进行差值。但对于本地VCO 来讲，一旦 VCO 器件选定，其固有频率就确定了。因此，我们可以将 VCO的自然振荡角频率产生的相位$w_{0}(t)$作为基准相位。

1.3 鉴相器PD

  1. 鉴相器原理

    不妨假设初始的输入信号表示为

    $$u_\mathrm{i}(t)=U_\mathrm{i}\sin[\omega_\mathrm{i}t+\theta_\mathrm{i}(t)]=U_\mathrm{i}\sin[\omega_\mathrm{0}t+(\omega_\mathrm{i}-\omega_\mathrm{0})t+\theta_\mathrm{i}(t)]$$

    令$\theta_1(t)=\Delta\omega_0t+\theta_\mathrm{i}(t)$，$\Delta\omega_\mathrm{o}=\omega_\mathrm{i}-\omega_0$，其中 $w_{0}$为输入信号与 VCO 自然角频率之间的固有角频率差。因此，环路的瞬时相差和频差可以用下式表示：$$\theta_\mathrm{e}(t)=\theta_1(t)-\theta_2(t)=\Delta\omega_\mathrm{o}t+\theta_\mathrm{i}(t)-\theta_2(t)$$

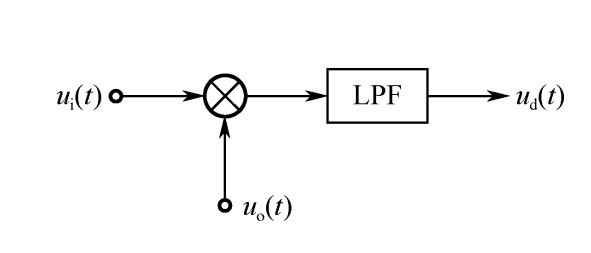
     鉴相器，顾名思义，是一个相位比较装置，用来检测输入信号相位$ \theta_1(t)$与反馈信号（ VCO输出信号）相位$\theta_2(t)$之间的相位差$\theta_e(t)$。输出的误差信号$u_\mathrm{d}(t)$是相差$\theta_e(t)$的函数。也就是说，只要某个装置的输出信号电压值的变化，能够直接反映相差$\theta_e(t)$的变化，就可以实现鉴相功能。当然，这种变化的转换最好具有线性的关系，否则分析和使用起来将十分复杂。实际上，鉴相器的特性可以是多种多样的，有正弦形特性、三角形特性、锯齿形特性等。鉴相器，它可用乘法器与低通滤波器的串接作为模型，其原理图如下所示：

    1712641565813.png

  2. 正弦鉴相器

    设乘法器的相乘系数为Km （这是一个无量纲的系数），输入信号$u_i(t)$与反馈信号$u_o(t)$ 相乘后的输出为$$\begin{aligned}K_\mathrm{m}u_\mathrm{i}(t)u_\mathrm{o}(t)& =K_\text{m}U_\text{i}\sin[\omega_\text{o}t+\theta_1(t)]U_\text{o}\sin[\omega_\text{o}t+\theta_2(t)] \&=-\frac12K_\text{m}U_\text{i}U_\text{o}\cos[2\omega_\text{o}t+\theta_1(t)+\theta_2(t)] \&+\frac12K_\text{m}U_\text{i}U_\text{o}\cos[\theta_1(t)-\theta_2(t)]\end{aligned}$$

    乘法器输出结果经过低通滤波器（ Low Pass Filter，LPF）滤除频率为$2w_0$的高频分量之后，得到误差电压为$$\begin{aligned}u_{\mathrm{d}}(t)&=\frac12K_\mathrm{m}U_\mathrm{i}U_\mathrm{o}\cos[\theta_1(t)-\theta_2(t)]\&=U_\mathrm{d}\cos\theta_\mathrm{e}(t)\end{aligned}$$

    其中$ U_d = \frac12K_\mathrm{m}U_\mathrm{i}U_\mathrm{o}$为鉴相器输出的最大电压。

  3. 余弦鉴相器

    它与正弦鉴相器的区别就在于它的输出$u_o(t)$，其推导过程如下： $$\begin{aligned}K_\mathrm{m}u_\mathrm{i}(t)u_\mathrm{o}(t)& =K_\text{m}U_\text{i}\sin[\omega_\text{o}t+\theta_1(t)]U_\text{o}\cos[\omega_\text{o}t+\theta_2(t)] \&=\frac12K_\text{m}U_\text{i}U_\text{o}\sin[2\omega_\text{o}t+\theta_1(t)+\theta_2(t)] \&+\frac12K_\text{m}U_\text{i}U_\text{o}\sin[\theta_1(t)-\theta_2(t)]\end{aligned}$$

    乘法器输出结果经过低通滤波器（ Low Pass Filter，LPF）滤除频率为$2w_0$的高频分量之后，得到误差电压为 $$\begin{aligned}u_{\mathrm{d}}(t)&=\frac12K_\mathrm{m}U_\mathrm{i}U_\mathrm{o}\sin[\theta_1(t)-\theta_2(t)]\&=U_\mathrm{d}\sin\theta_\mathrm{e}(t)\end{aligned}$$

    其中$ U_d = \frac12K_\mathrm{m}U_\mathrm{i}U_\mathrm{o}$为鉴相器输出的最大电压。

  4. $u_d(t)$求解

    针对正余弦鉴相器的输出不同，我们需要对正弦鉴相器角度进行转化，令$\theta_{\mathrm{el}}(t)=\theta_{\mathrm{e}}(t)+\pi/2$，$\theta_{21}(t)=\theta_2(t)-\pi/2$，则正弦鉴相器的输出就有如下变换：$$\begin{aligned}u_{\mathrm{d}}(t)&=U_{\mathrm{d}}\cos\theta_{\mathrm{e}}(t)\&=U_{\mathrm{d}}\cos[\theta_{\mathrm{el}}(t)-\pi/2]\&=U_{\mathrm{d}}\sin\theta_{\mathrm{el}}(t)\end{aligned}$$

    其中：$\theta_{\text{е}1}(t)=\theta_1(t)-\theta_{21}(t)$

    通过转化之后，无论是正余弦，他们都可以满足正弦鉴相器曲线。

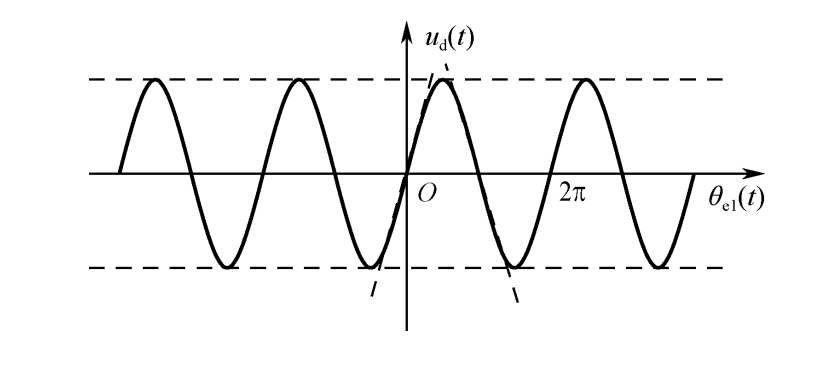
    1712645184469.png

    仔细观察一下正弦曲线，在一个$2\pi$周期内，可以将线分为两段来处理：$(-\pi/2,\pi/2)$ 和$(\pi/2,3\pi/2)$。上升段可以近似成斜率为Ud 的直线，下降段可以近似成斜率为－ Ud 的直线（实际上，只有当环路工作在锁定状态时，鉴相特性处在零度附近，正弦特性才具有最佳的线性特性）。当 $-\pi/2<\theta_{\mathrm{el}}(t)<\pi/2$时，输出可近似为：$$u_{\mathrm{d}}(t)=U_{\mathrm{d}}\sin\theta_{\mathrm{el}}(t)\approx U_{\mathrm{d}}\theta_{\mathrm{el}}(t)$$

1.4 环路滤波器LF

 简单说来，环路滤波器是将鉴相器输出含有纹波的信号平均化，将此变换为交流成分少的直流信号的低通滤波器。实际上，环路滤波器确实是一个低通滤波器，但不仅仅是普通的低通滤波器， 除了完成低通滤波功能外，还有一种重要作用，即决定整个 PLL 电路的传输特性，进而决定 PLL 电路的稳定性、捕获带宽、捕获速度等几乎所有的重要特性。

 因此，环路滤波器的作用有两点：一是低通滤波器作用，且通带要远低于鉴相器的带宽，因为 VCO 只有在输入纹波小的直流信号时，才能输出寄生成分小的高质量正弦信号；二是控制环路特性，并且这才是环路滤波器的主要功能。再进一步讲，对于电子工程师来讲，所谓锁相环电路设计，其实就是在设计环路滤波器而已。

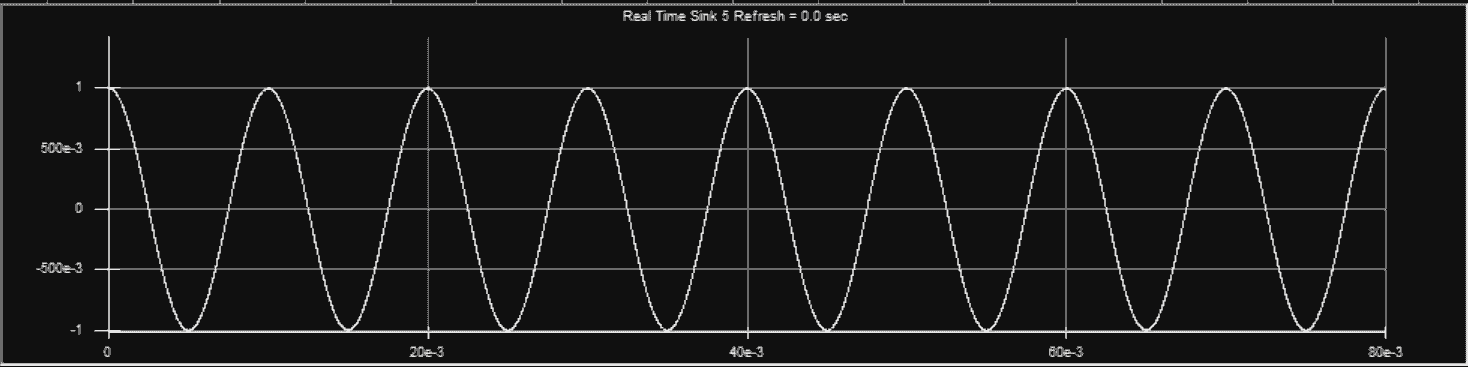
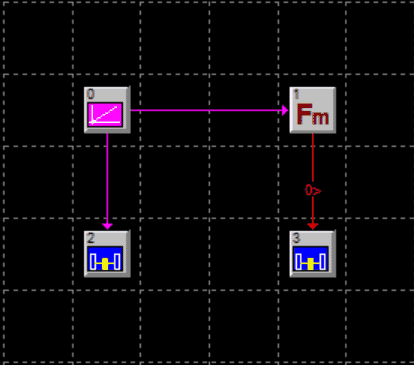
二. 最简单锁相环的SystemView仿真

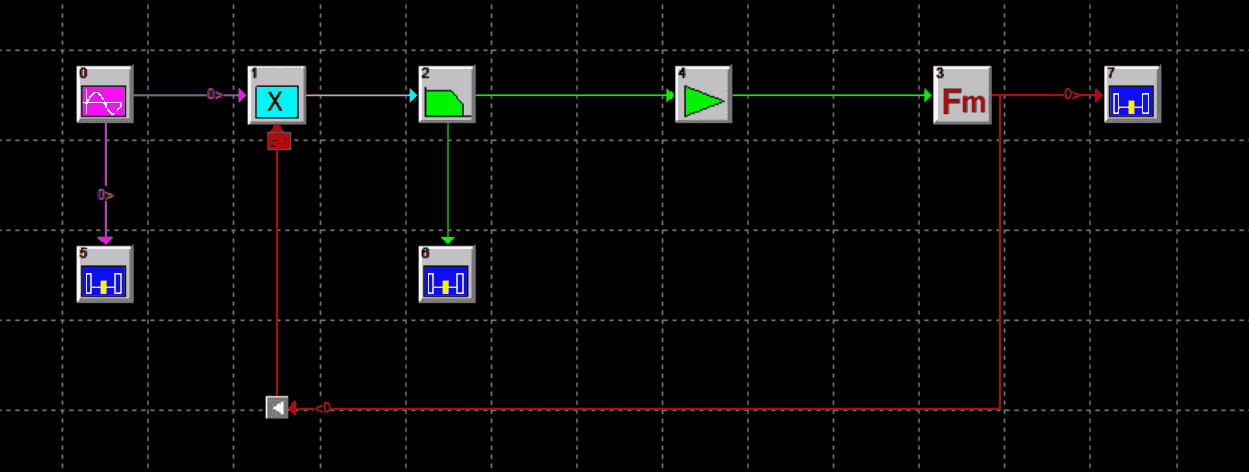
1712646251810.png
相位相同
元件参数
信号源Amplitude=1 V； Fequency=100 Hz； Phase=0；
乘法器----
低通滤波器Design Filters=Analog； Filter Type=Chebyshev； No.of Poles=4； Low Cuttoff=150 Hz； Filter Pass-Band=Lowpass； Inband Ripple=0.1 dB
增益放大器Gain Units=Linear； Gain=1
VCOAmplitude=1 V； Fequency=100 Hz； Phase=0； Mod Gain=100 Hz/V
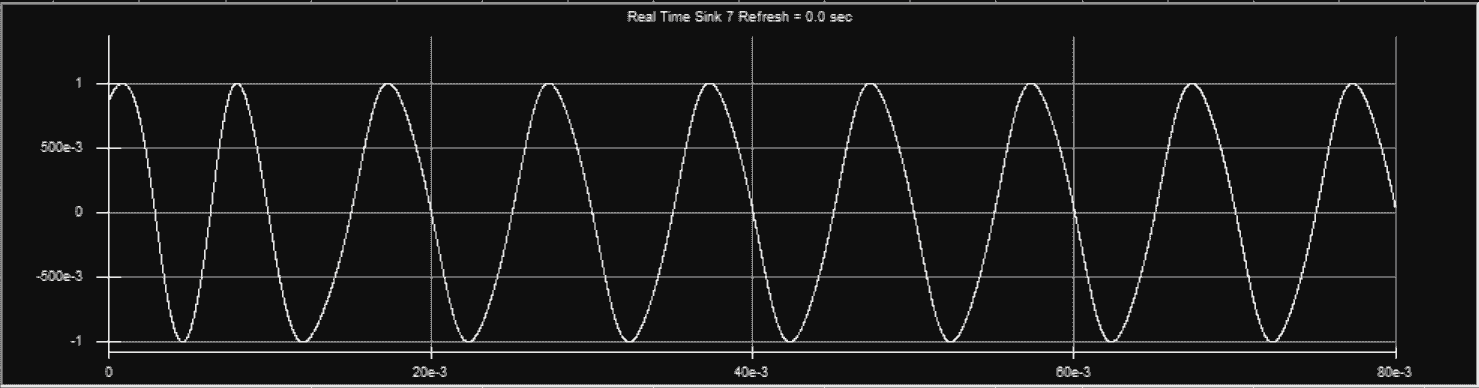
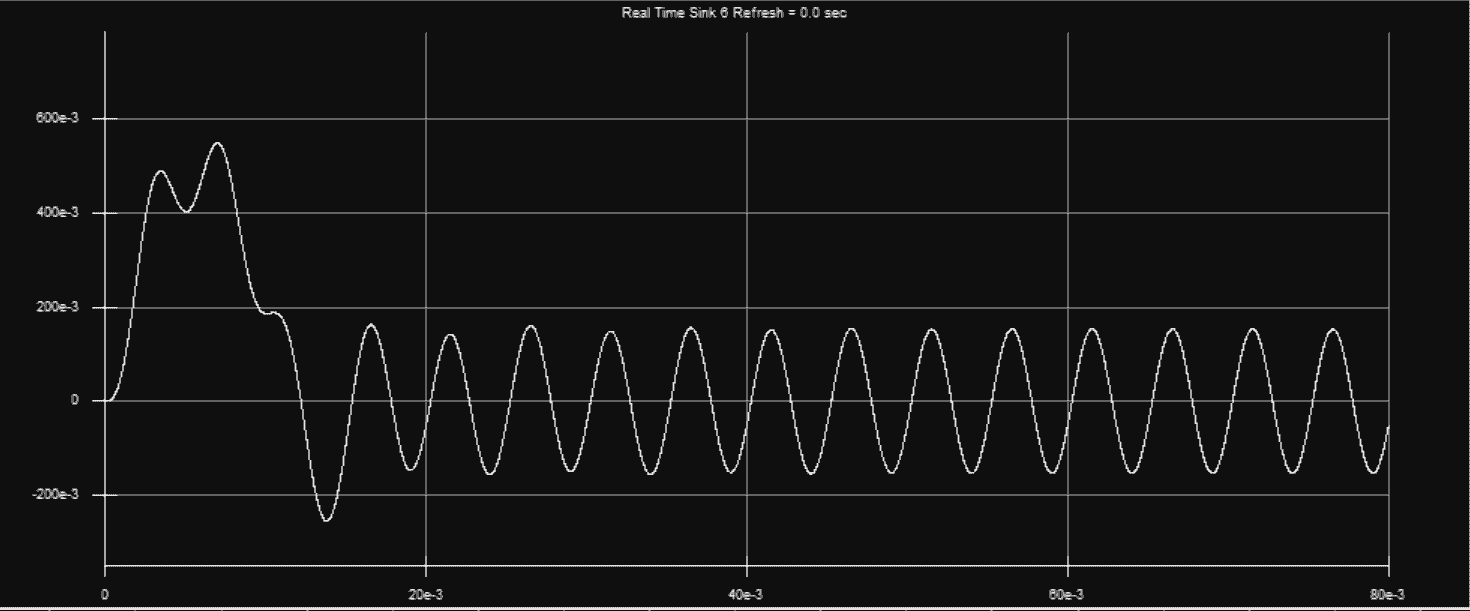
相位不同
元件参数
信号源Amplitude=1 V； Fequency=100 Hz； Phase=90；
乘法器----
低通滤波器Design Filters=Analog； Filter Type=Chebyshev； No.of Poles=4； Low Cuttoff=150 Hz； Filter Pass-Band=Lowpass； Inband Ripple=0.1 dB
增益放大器Gain Units=Linear； Gain=1
VCOAmplitude=1 V； Fequency=100 Hz； Phase=60； Mod Gain=100 Hz/V
相位相同
1712646846086.png1712646822811.png1712646796092.png
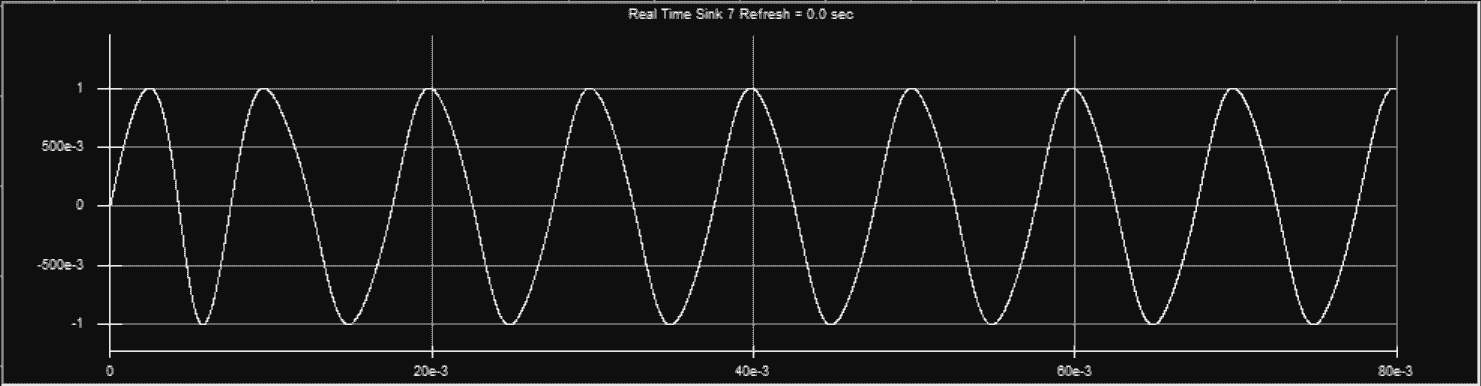
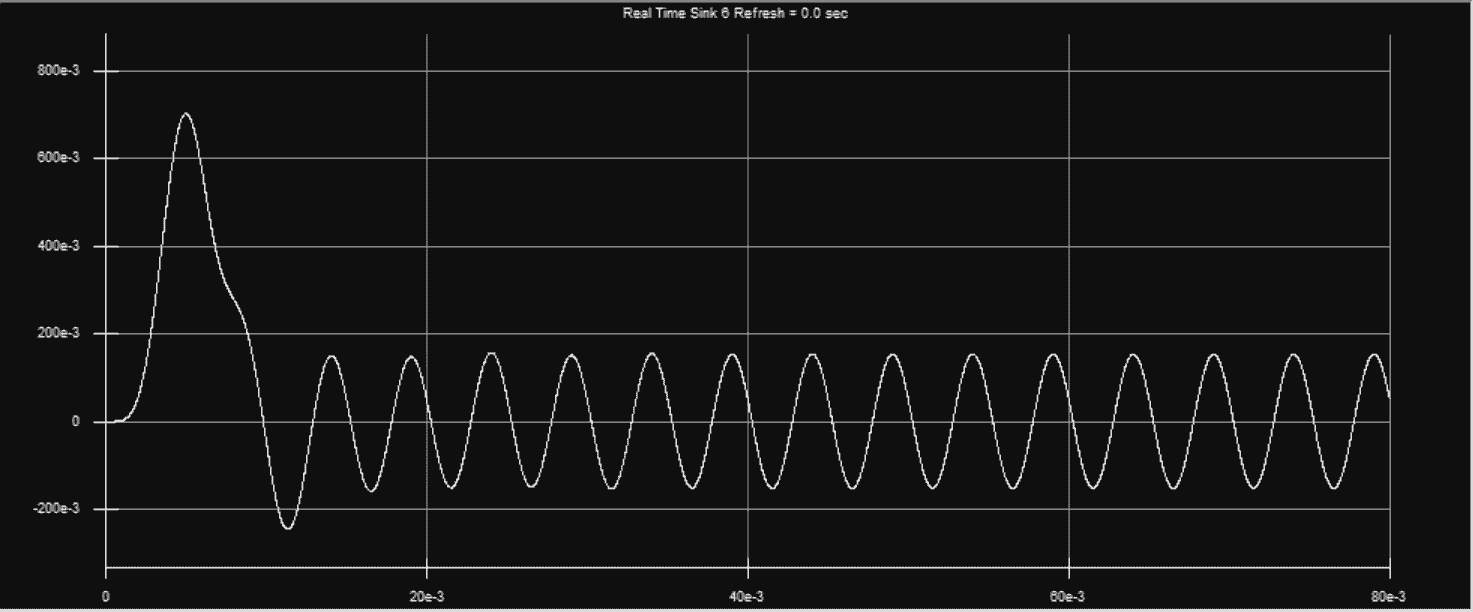
相位不同
1712647037396.png1712647053800.png1712647015404.png

最后说

教材PDF下载