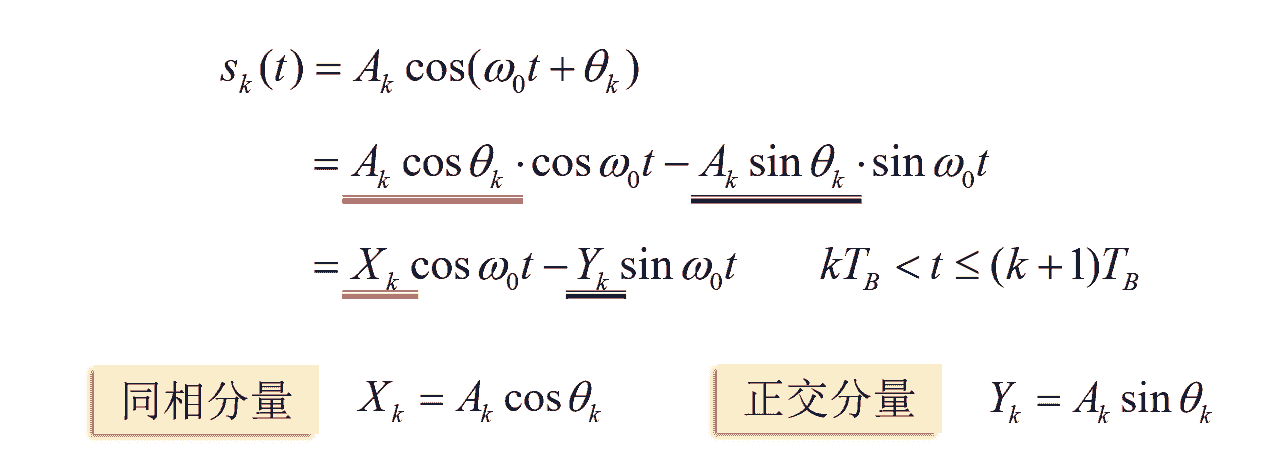🌈以下是本人对《通信原理》第七章 数字频带传输系统的学习，是为了方便后续的学习，如有补充和错误，欢迎评论区留言！相关参考资料和视频已放在文末。

一.二进制数字调制、解调原理：2ASK、2FSK

1.1二进制振幅键控：2ASK

  1. 二进制振幅键控原理 ASK: Amplitude Shift Keying
    • 用二进制数字基带信号控制正弦载波的幅度（两种幅度）。即“0”---->0，“1”---->$cosw_{c}t$
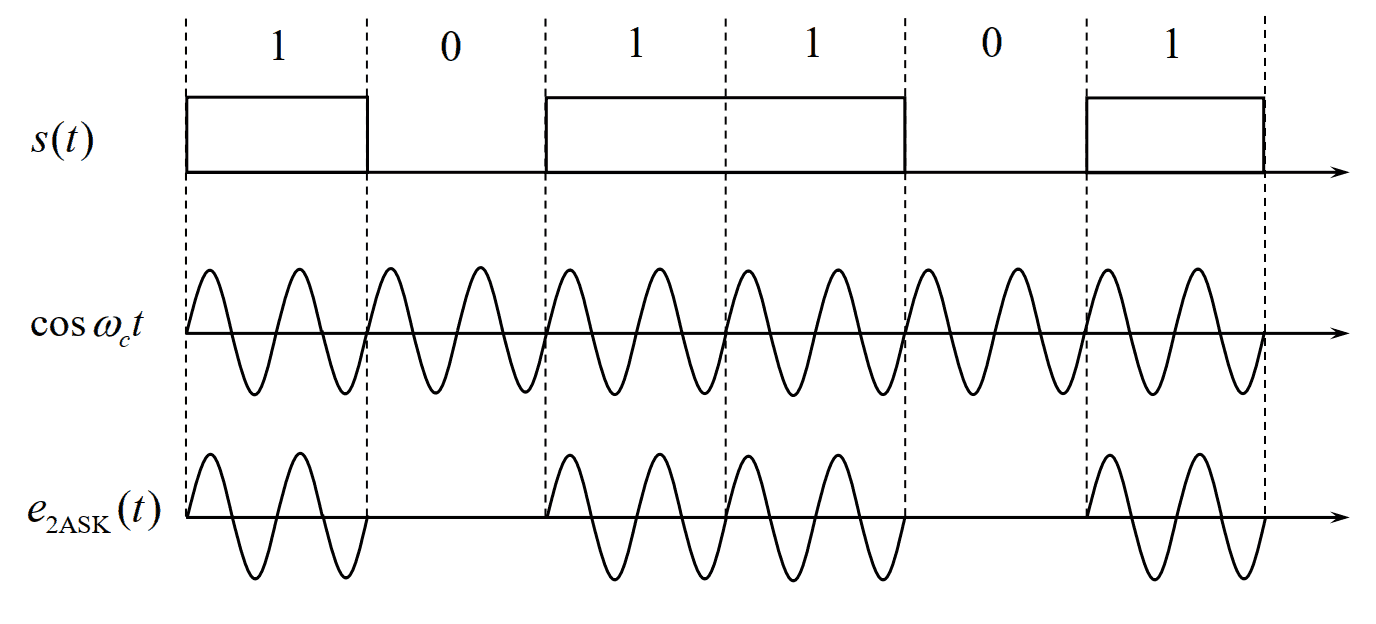
    • 波形表示：1711953055767.png
    • 2ASK信号表达式：$e_{2ASK}=s(t)cosw_{c}t$，其中$s(t)$信号为单极性基带信号。
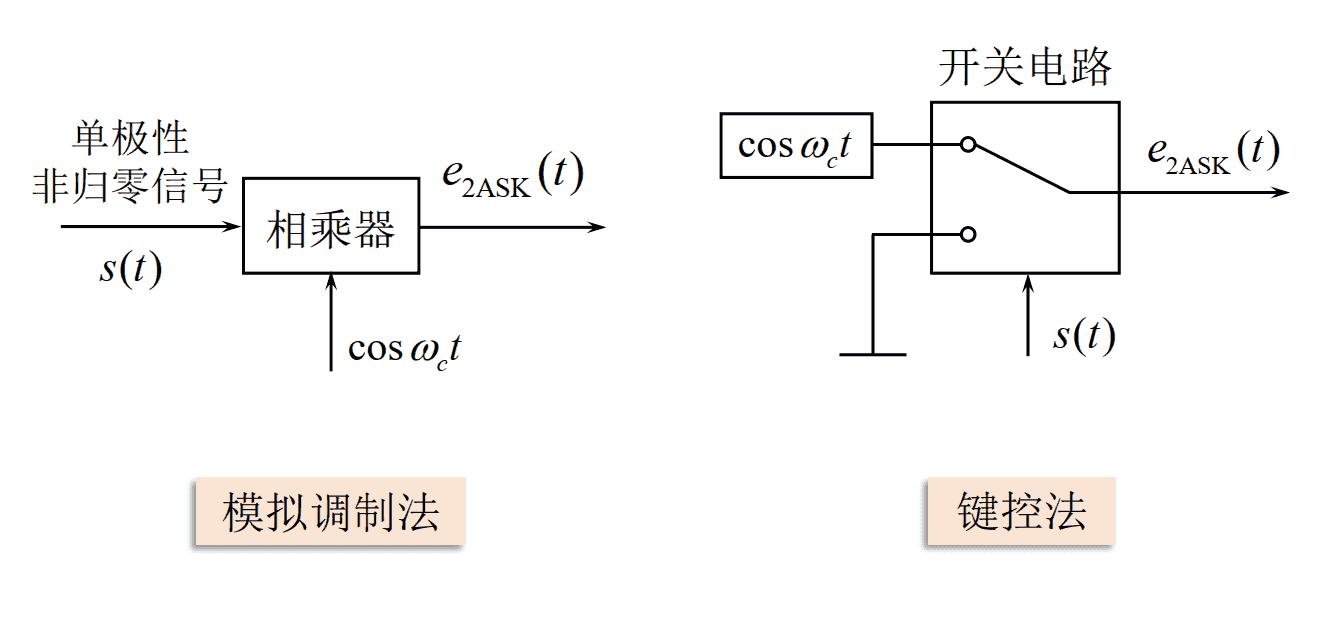
    • 2ASK信号产生方法：1711953611413.png
  2. 2ASK信号解调方法
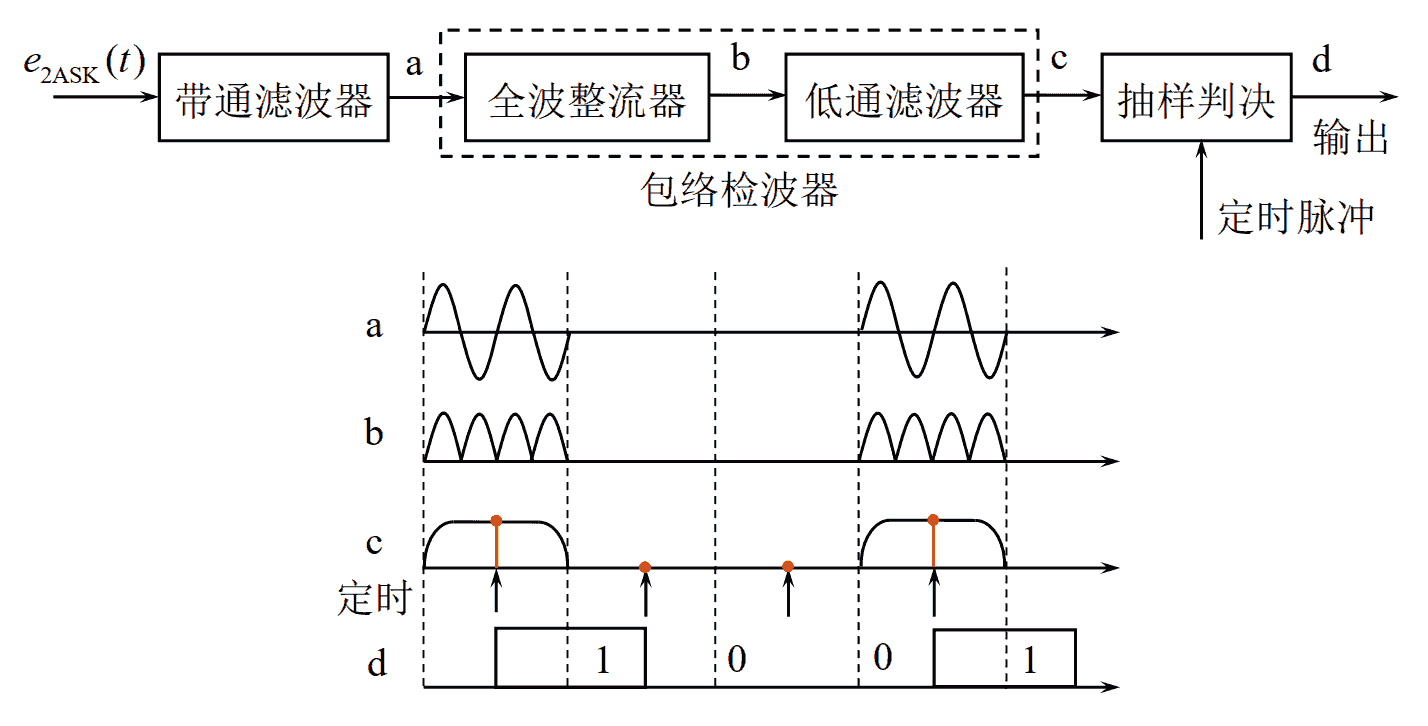
    1. 包络检波法/非相干解调法：1711954064398.png
    2. 相干解调法/同步检波法：1711954270164.png

1.2 二进制频移键控

  1. 二进制频移键控原理 FSK: Frequency Shift Keying
    • 用二进制数字基带信号控制正弦载波的频率（两种频率）。即“0”---->$cosw_1t$，“1”---->$cosw_2t$。
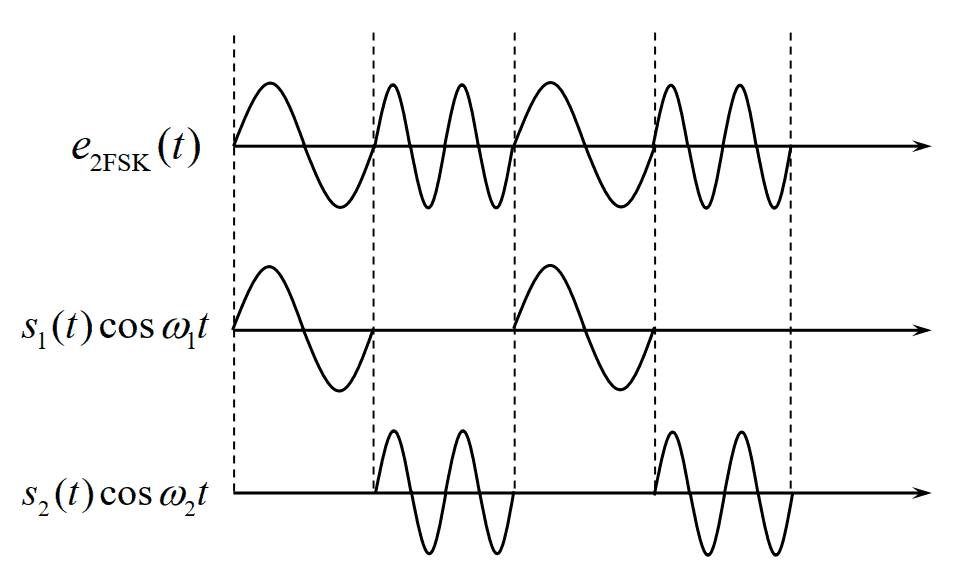
    • 2FSK信号波形表示：1711954734318.png
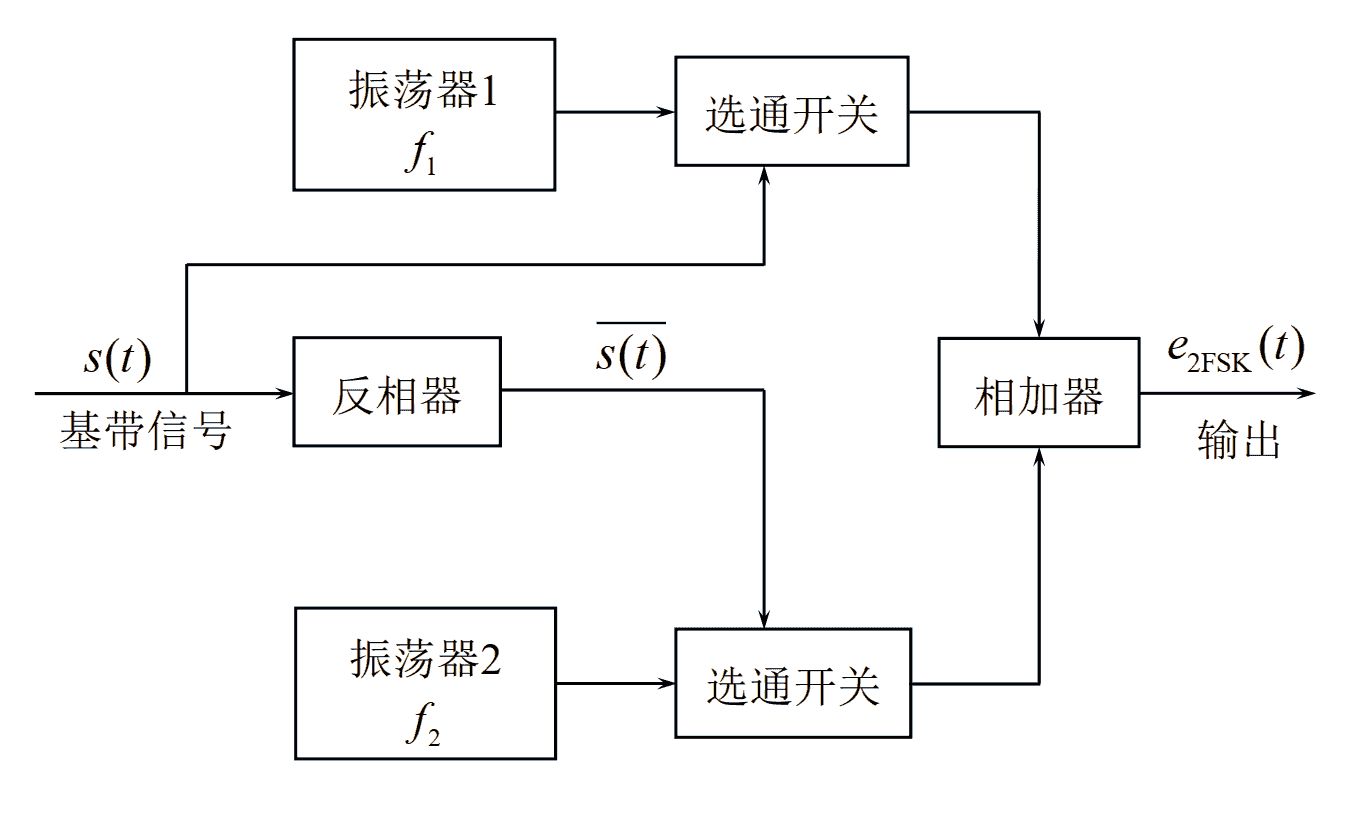
    • 2FSK信号产生方法：1711954809019.png
  2. 2FSK信号解调方法
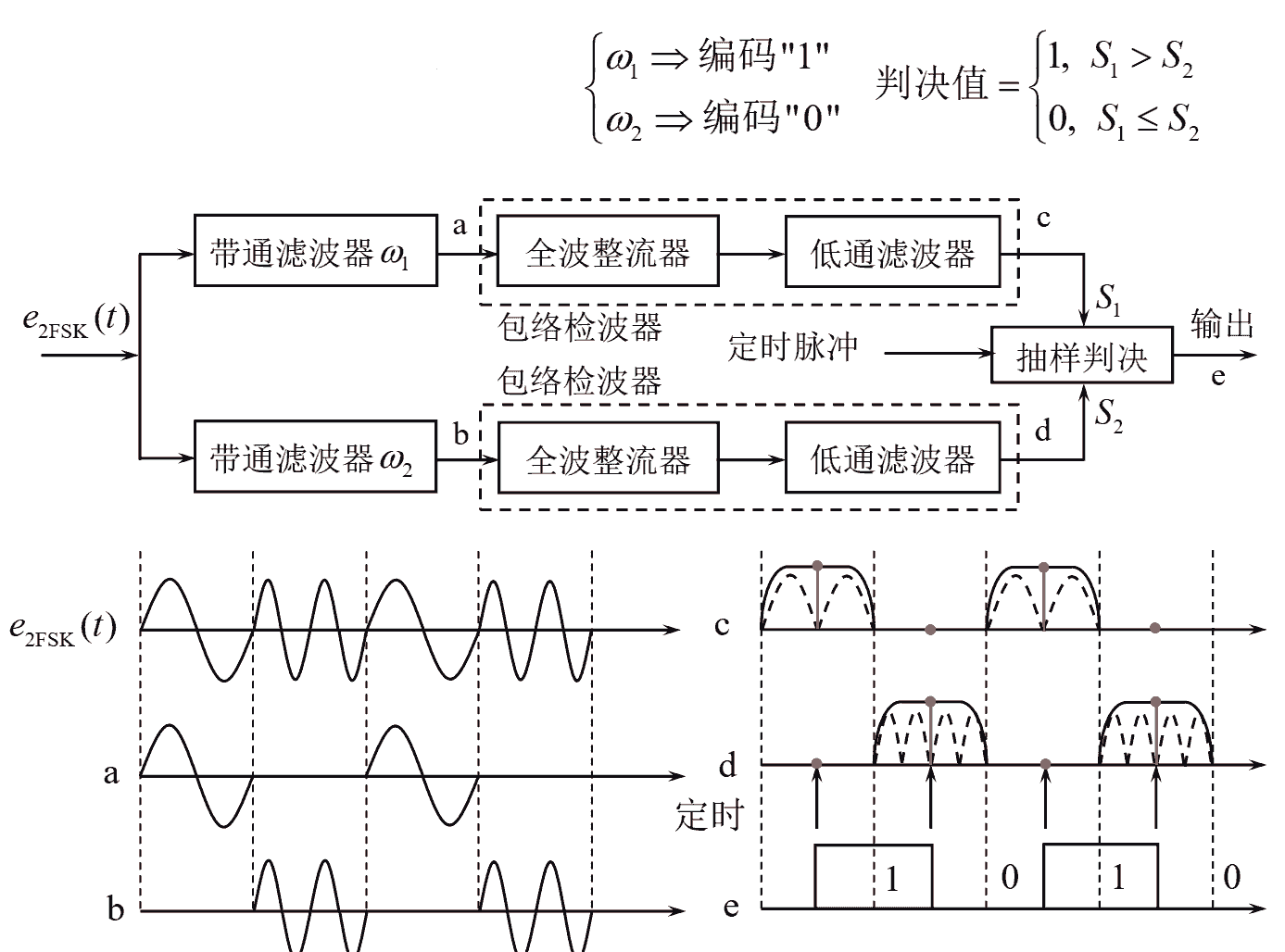
    1. 包络检波法/非相干解调法：1711955006901.png
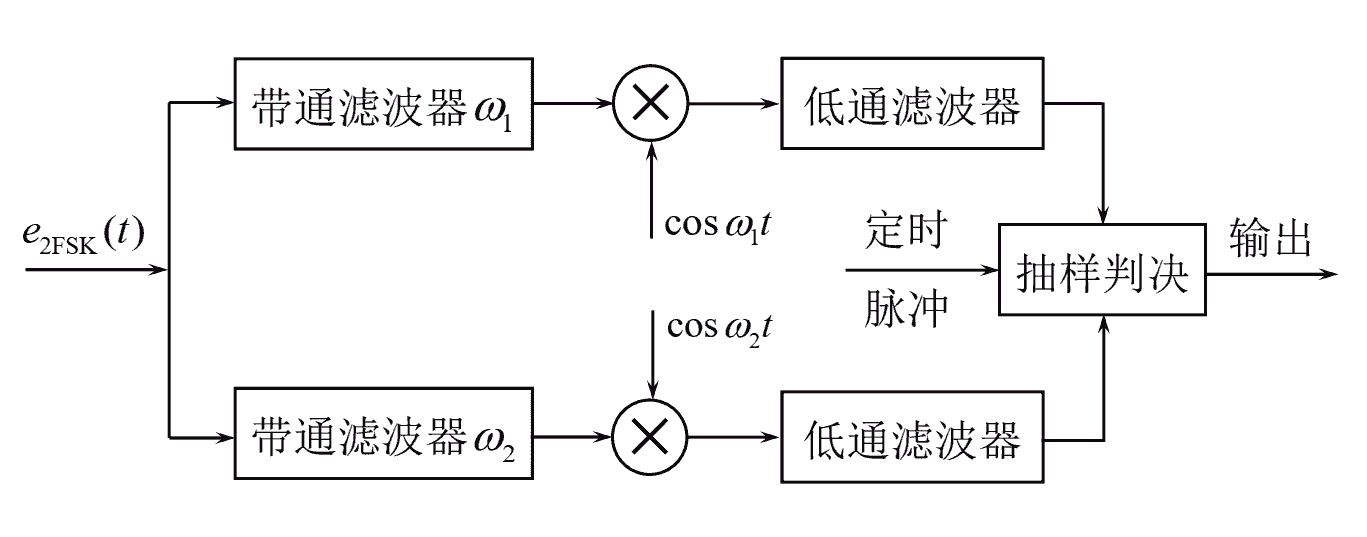
    2. 相干解调法/同步检波法：1711955078515.png

二.二进制数字调制、解调原理：2PSK、 2DPSK

2.1 二进制相移键控： 2PSK

  1. 二进制相移键控原理 PSK: Phase Shift Keying

    • 用二进制数字基带信号控制正弦载波的相位（两种相位）。即“0”---->0相位，“1”---->$\pi$相位。

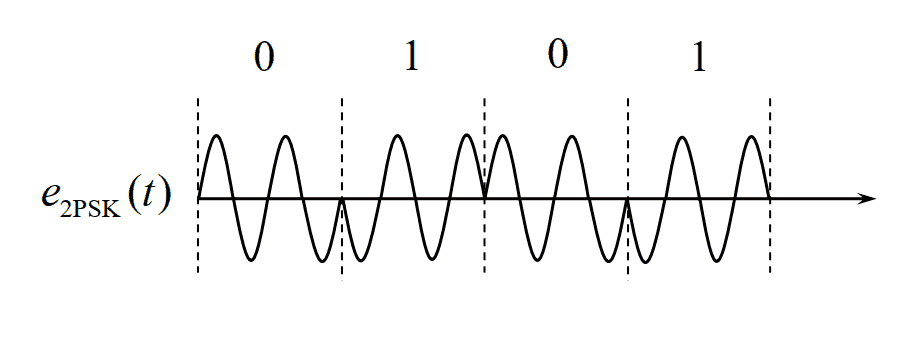
    • 2PSK信号波形表示：1711955497934.png

    • 2PSK信号表达式：

      $$e_{2\mathrm{PSK}}(t)=A\cos(\omega_ct+\varphi_n),\quad\varphi_n=\begin{cases}0&\text{编码}0\\pi&\text{编码}\pi\end{cases}$$

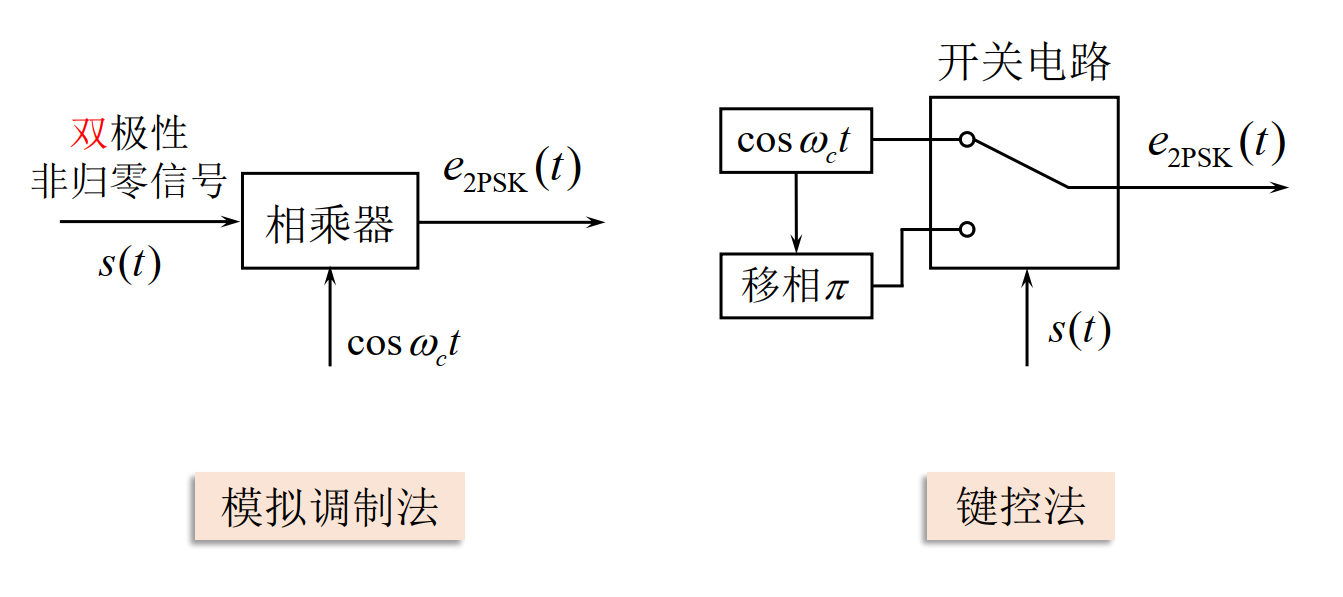
    • 2PSK信号产生方法：1711955785395.png

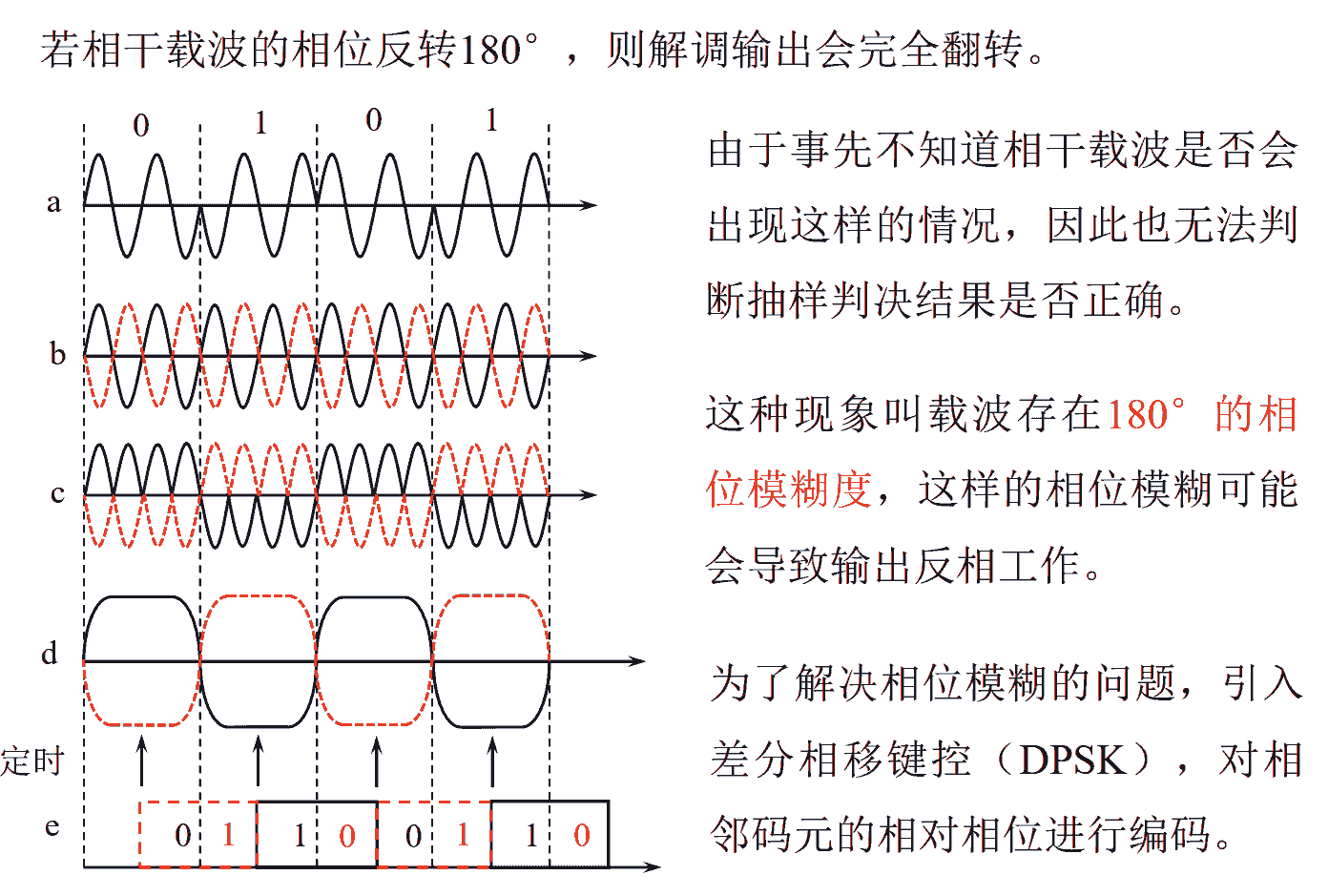
  2. 2PSK信号解调方法

    1711955838038.png

  3. 2PSK调制存在的问题

    1711955972956.png


2.2 二进制相移键控： 2DPSK

  1. 二进制差分相移键控原理 DPSK: Differential PSK

    利用前后相邻码元的载波相对相位表示信息。$\Delta\boldsymbol{\varphi}=\boldsymbol{\varphi}n-\boldsymbol{\varphi}{n-1}=\begin{cases}0&\text{编码”}0\text{"}\[2ex]\pi&\text{编码“}1\text{”}&\end{cases}$

  2. 2PSK和2DPSK信号区别

    • 2PSK信号：作为绝对调相，与基准载波进行相位比较。
    • 2DPSK信号：作为相对调相，则与前一个码元的载波相对相位进行比较。

  3. 2DPSK信号相位举例

    二进制数字信息 1 1 0 1 0
    2DPSK信号相位(参考相位为0) (0) $\pi$ 0 0 $\pi$ $\pi$
    2DPSK信号相位(参考相位为$\pi$) （$\pi$） 0 $\pi$ $\pi$ 0 0

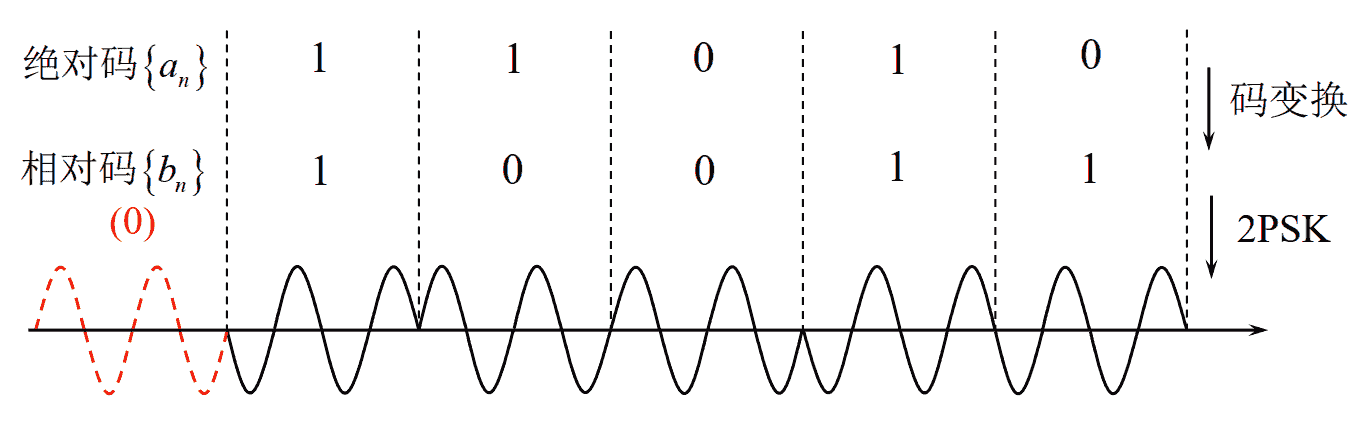
  4. 2DPSK信号的编码规则与波形

    先对绝对码进行码变换， 编为相对码， 再进行2PSK绝对调相。设绝对码为$\left{a_n\right}$， 相对码为$\left{b_n\right}$。

    编码规则：$\begin{aligned}b_n=a_n\oplus b_{n-1}\end{aligned}$， 译码规则： $\begin{aligned}a_n=b_n\oplus b_{n-1}\end{aligned}$1712026724079.png

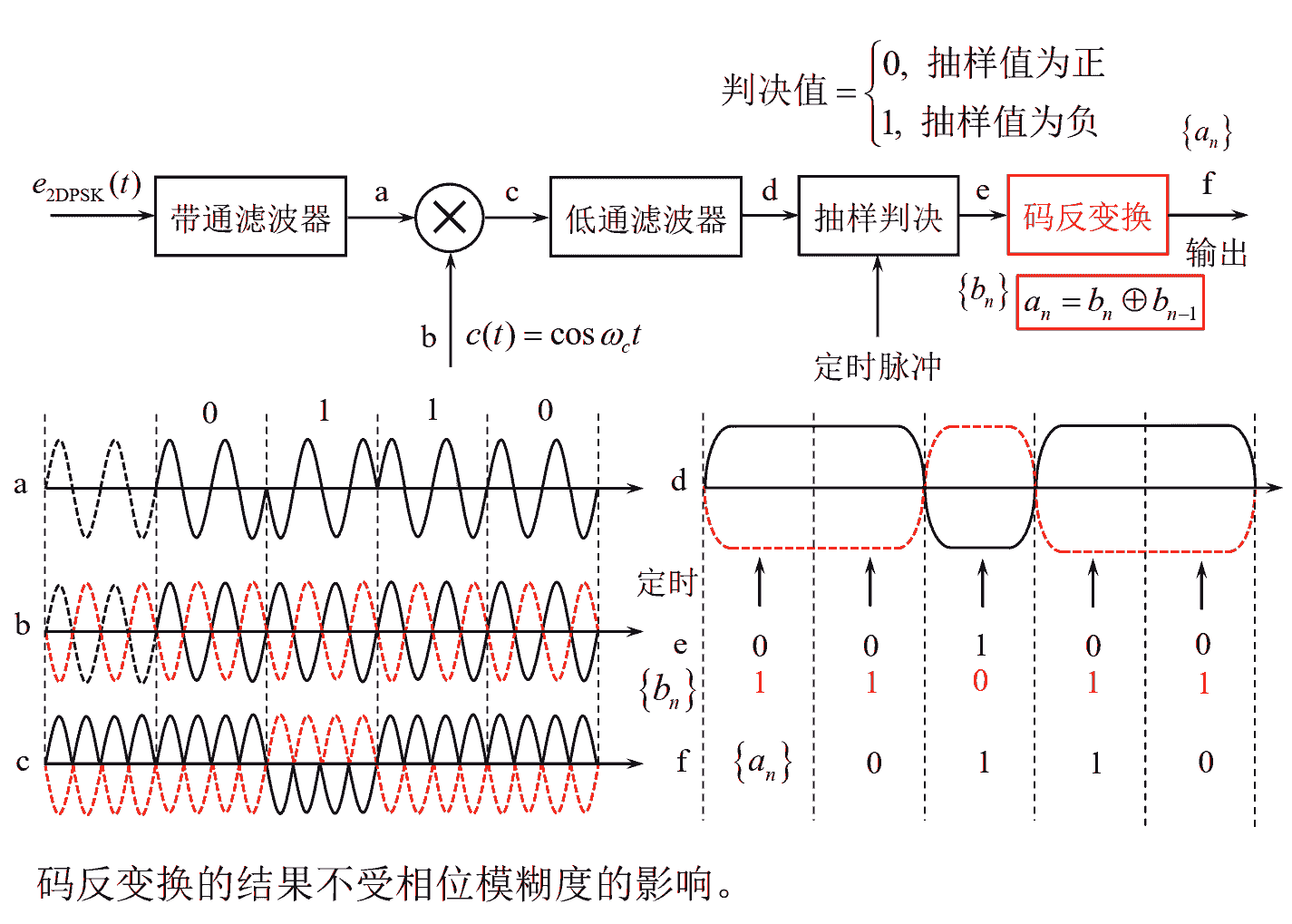
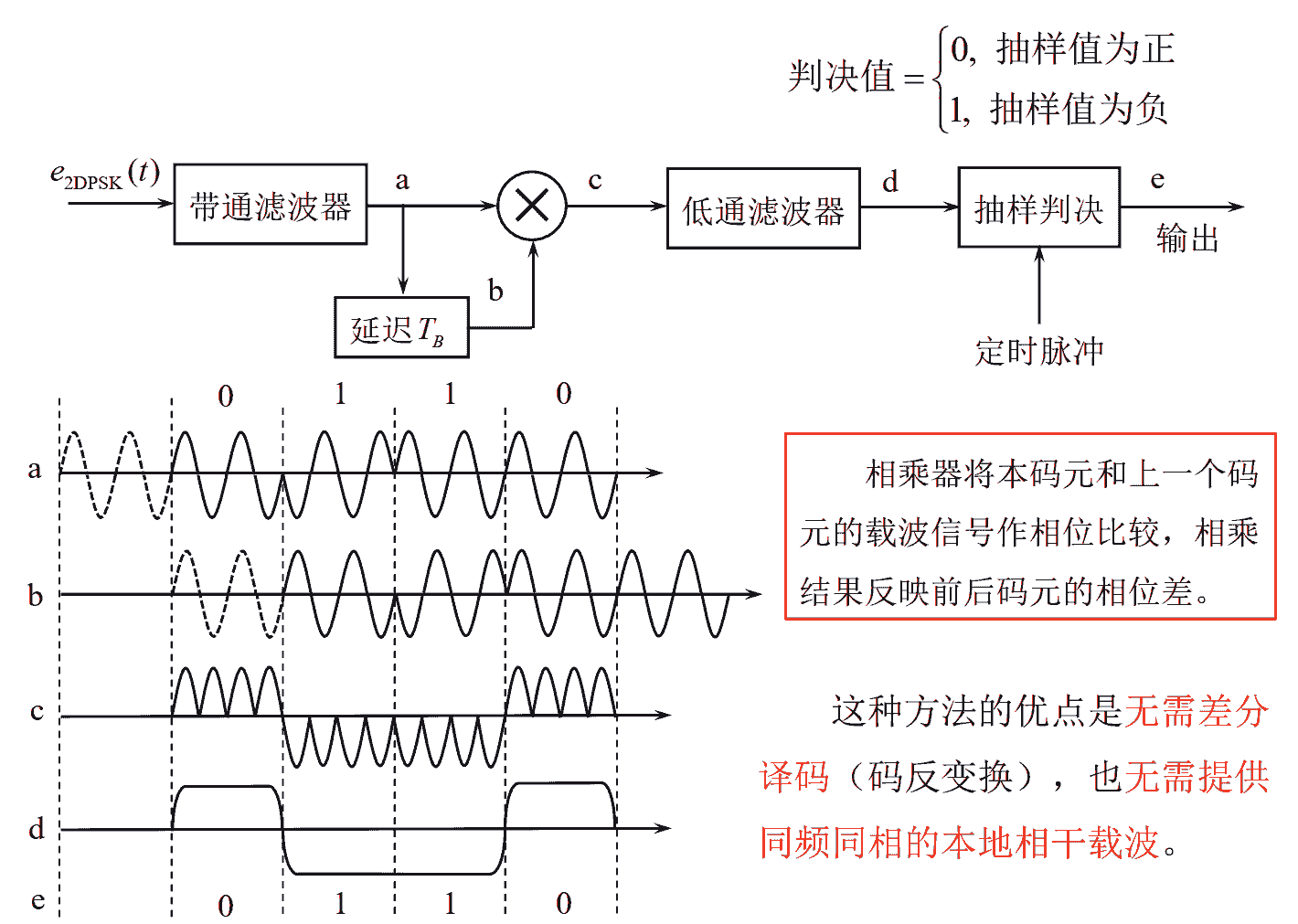
  5. 2DPSK信号解调方法

    1. 相干解调（极性比较） + 码反变换

      1712034594246.png

    2. 差分相干解调（相位比较法）

      1712034722460.png

三.多进制数字调制

3.1 多进制数字调制概述

  1. 多进制数字调制优点

    1
    由于二进制码元只携带1bit信息，多进制码元携带$log_2 M bit$信息在二进制数字调制的基础上，推广到多进制调制$R_B=\frac{R_b}{\log_2M}$，比特率$R_b$给定时，增大调制进制数M，可降低符号率$R_b$，从而降低信号带宽，节约传输资源。数据率$R_B$给定时，增大调制进制数M ，可以提高比特率 ，从而提高频带利用率$\eta_b$ 。

  2. 多进制数字调制缺点

    但相应的代价是判决范围减小引起的系统误码率增加，以及系统复杂度的增加。1712039582989.png

3.2 多进制振幅键控原理： MASK

  1. MASK信号波形及表达式（4ASK为例）

    $$e_\text{МАSK}{ ( t ) }=s(t)\cos\omega_{c}t$$

    1712039763325.png

  2. MASK信号产生方法及解调方法

    1712040017798.png

    MASK的解调方法与2ASK相似，有相干、非相干两种解调方法，但在结尾需添加“M-2电平转换” 环节。

3.3 多进制频移键控原理： MFSK

  1. MFSK信号波形及表达式（4FSK为例）

    $$e_{\mathrm{MFSK}}(t)=\sum_nAg(t-nT_B)\cos\omega t\quad i=1,2,\cdots,M$$

    1712040324108.png

    表达式中矩形脉冲部分幅度恒定，变化的是载波频率，各载波频率为$f_i=f_c+i\Delta f$，频率间隔$\Delta f=f_i-f_{i-1}$。

    因此，$$e_{\mathrm{MFSK}}(t)=\sum_nAg(t-nT_B)\cos(\omega_ct+2\pi i\Delta ft)$$

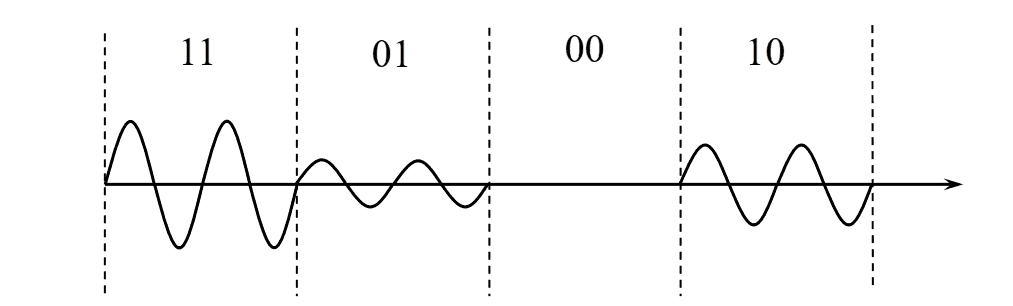
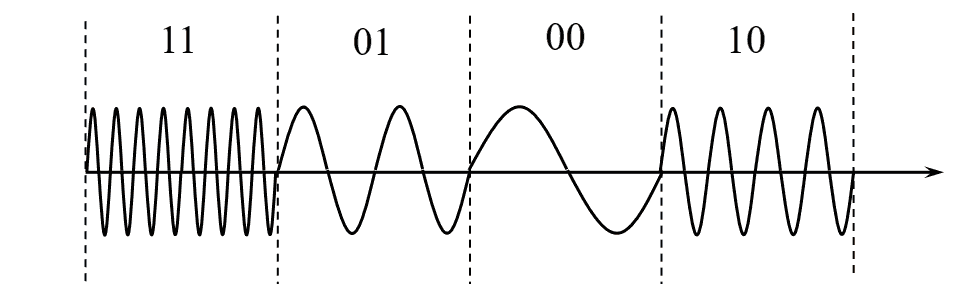
3.4 多进制相移键控： MPSK

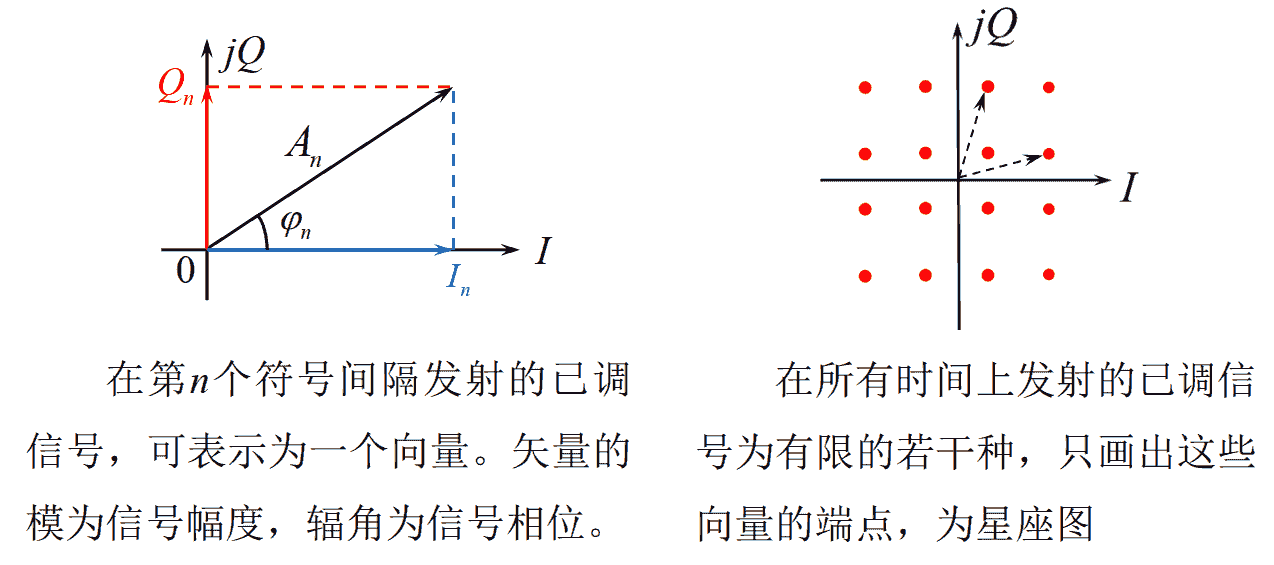
  1. 正交调制原理

    1712042376841.png

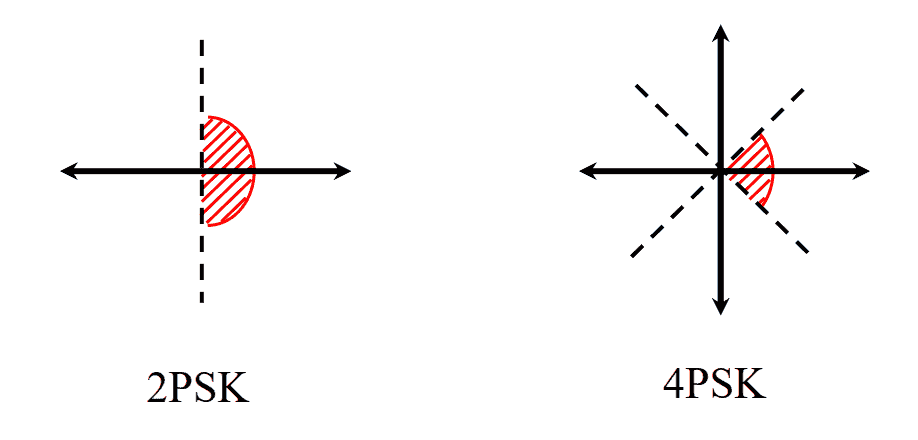
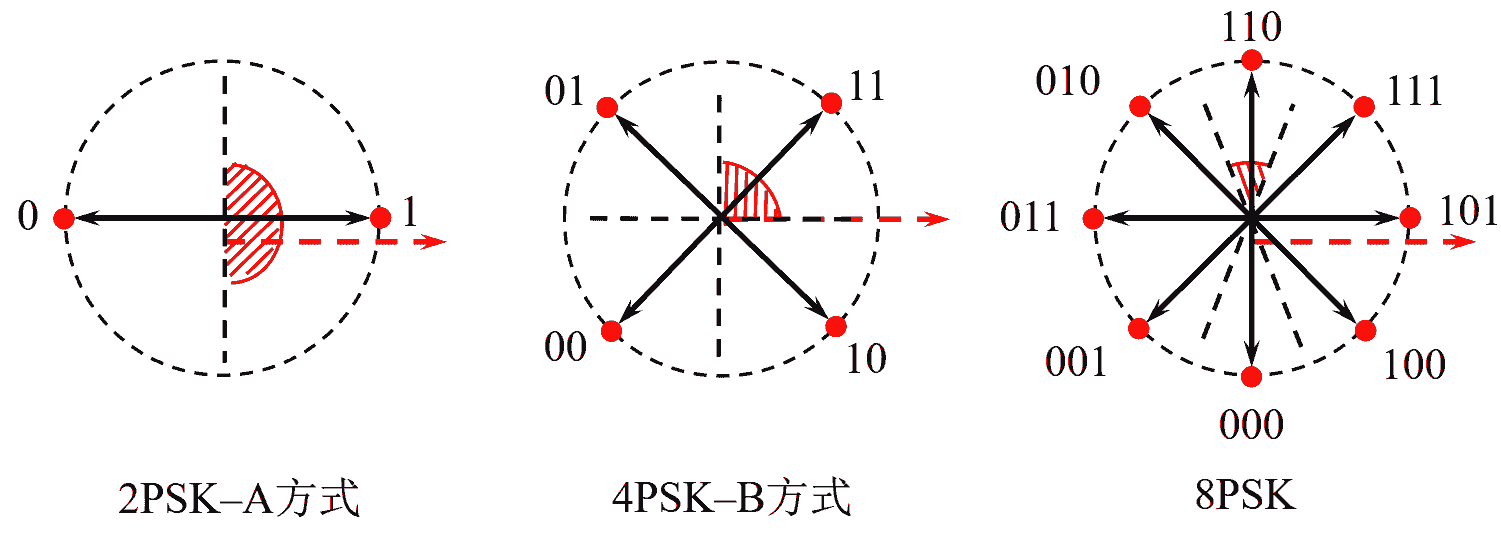
  2. 信号矢量图/星座图

    1712042474111.png

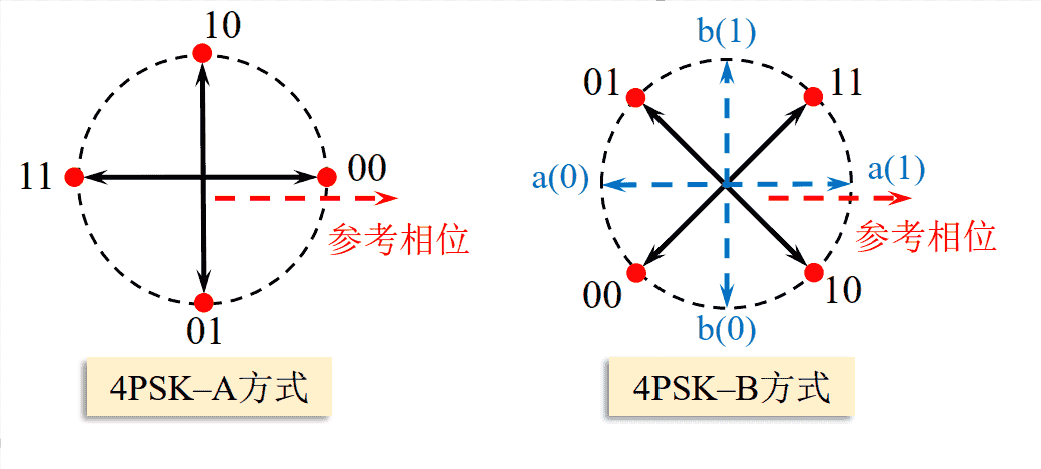
  3. 四进制相移键控4PSK/QPSK

    1. 4PSK有两种调制方式： A方式和B方式。

      1712043132145.png

      1712042937104.png

    星座点的编码排布满足格雷码， 即相邻码组的距离为1， 这样排的好处是如果发生错码， 错到相邻的码组只错1bit。

3.5 多进制差分相移键控：MDPSK

  1. 四进制差分相移键控4DPSK调制方式

    它的调制方式是DPSK和MPSK两种方式的结合，既有MPSK减小带宽的优势，又克服了载波相位模糊。

四.几种现代调制方式简介

4.1. 正交振幅调制： QAM

  1. 需求背景

    在MPSK调制中，提高进制数M可以有效提高频带利用率，但是由于相邻信号点的距离减小，故噪声容限降低，难以保证误码性能。需要一种有效的调制方式，来改善高进制情况下系统的抗噪声性能，提高频带利用率。1712044125797.png

  2. 设计思想

    • 增大信号距离，即增加圆周半径。意味着增大信号的功率，这在发射功率受限的环境下难以实现。
    • 不增大圆周半径，即信号功率，但重新安排星座点的位置。
    • QAM调制的思想就是后者，它是一种振幅和相位联合键控的调制方式，因此又称为APK调制。

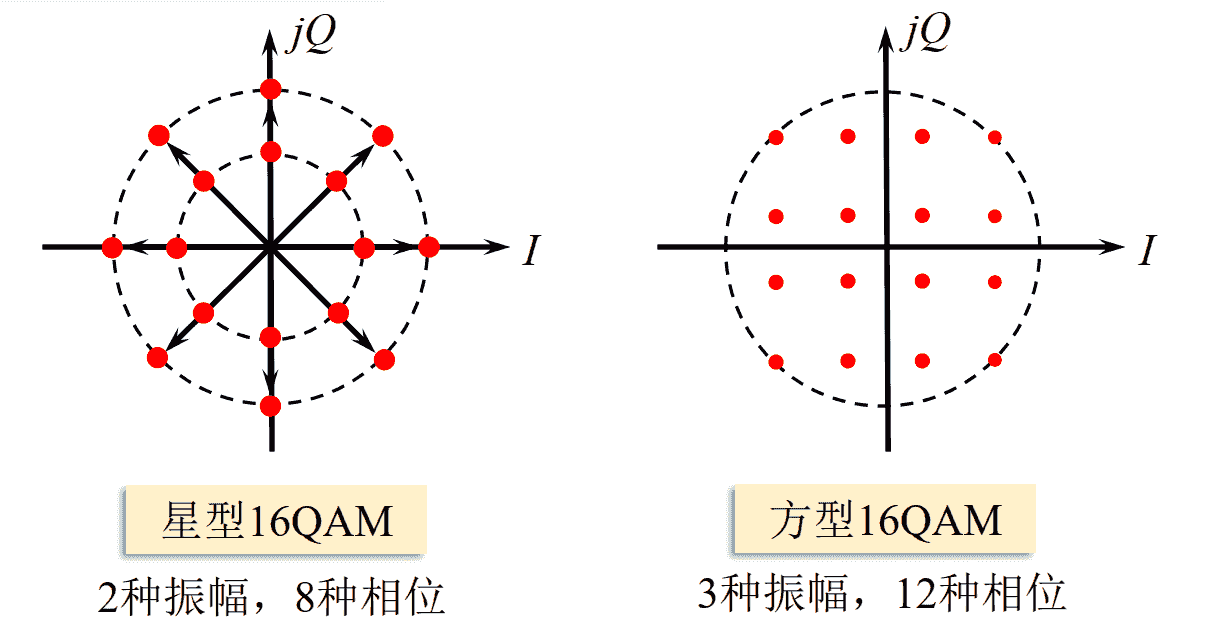
  3. 16QAM信号的星座图

    1712044579390.png

    多径衰落信道中， 信号的振幅、 相位取值越多， 受到的影响越大，故星型16QAM比方型16QAM更具备吸引力。方型16QAM信号的产生与接收更容易实现， 故实际应用更广泛。

  4. 16QAM信号的产生

    在QAM调制中，载波的振幅、相位同时受基带信号控制。

    单个码元的表达式为：
    1712046613580.png

    16QAM调制可看作两路正交的4ASK信号之和，符合正交调制特性。