通信原理学习之路:第五章 模拟调制系统
🌈以下是本人对《通信原理》第五章 模拟信号调制的学习,是为了方便后续的学习,如有补充和错误,欢迎评论区留言!相关参考资料和视频已放在文末。
第五章 模拟信号调制
一.模拟信号调制概述
1.1 调制的定义
- 调制:把消息信号寄托在载波的某个参数上,形成已调信号。
- 解调:调制的逆过程,从已调信号中恢复消息信号。
1.2 调制的目的
- 匹配信道特性,减小天线尺寸,提高辐射效率;其中频率越高,天线尺寸越小。
- 通过频谱搬移,实现信道的多路复用,提高信道利用率;
- 扩展信号带宽,提高系统的抗干扰能力;
- 实现带宽与信噪比的互换(有效性与可靠性的互换)。
1.3 调制的分类
- 按消息信号$m(t)$类型分类:模拟调制、数字调制。
- 按已调信号频谱结构分类:
- 线性调制:AM、DSB、SSB、VSB
- 非线性调制:FM、PM
二.线性调制:AM、DSB、SSB和VSB
2.1 幅度调制AM
-
AM调制原理图
-
AM调制须满足的条件
$m(t)$均值为0:
$$\overline{m(t)}=\lim_{T\to\infty}\frac1T\int_{-T/2}^{T/2}m(t)\mathrm{d}t=0$$调幅系数:$a=\frac{\left|m(t)\right|_{\max}}{A_0}$,${a\leq1}$
-
表达式
-
时域表达式$$s_{\mathrm{AM}}(t)=\left[A_0+m(t)\right]\cos\omega_{c}t=A_0\cos\omega_{c}t+m(t)\cos\omega_{c}t$$
其中$A_0\cos\omega_{c}t$为载波项,$m(t)\cos\omega_{c}t$边带项。
-
频域表达式$$S_{\mathrm{AM}}(\omega)=\pi A_0\left[\delta(\omega+\omega_{c})+\delta(\omega-\omega_{c})\right]+\frac1 2\left[M(\omega+\omega_{c})+M(\omega-\omega_{c})\right]$$
其中$\pi A_0\left[\delta(\omega+\omega_{c})+\delta(\omega-\omega_{c})\right]$为载波项,$\frac1 2\left[M(\omega+\omega_{c})+M(\omega-\omega_{c})\right]$为边带项。
-
-
在不同调幅状态下AM信号时域波形变化
-
AM信号的调制效率
-
AM信号的特点
- 调幅系数$a=\frac{\left|m(t)\right|_{\max}}{A_0}\leq1$时,包络与$m(t)$成正比;
- 已调信号带宽:$B_{\mathrm{AM}}=2f_H$,其中$f_H$是$m(t)$信号的最大频率。
- 已调信号功率:$P_{\mathrm{AM}}=\frac{A_0^2}2+\frac{\overline{m^2(t)}}2=P_C+P_S$。
- 功率利用率低:最大利用率小于50%,在单频余弦满调幅情况下,最大利用率为1/3。
2.2 双边带调制DSB
-
DSB调制原理图
-
DSB信号的时域表达式及波形图
-
时域表达式:$$s_{\mathrm{DSB}}(t)=m(t)\cos\omega_ct$$
-
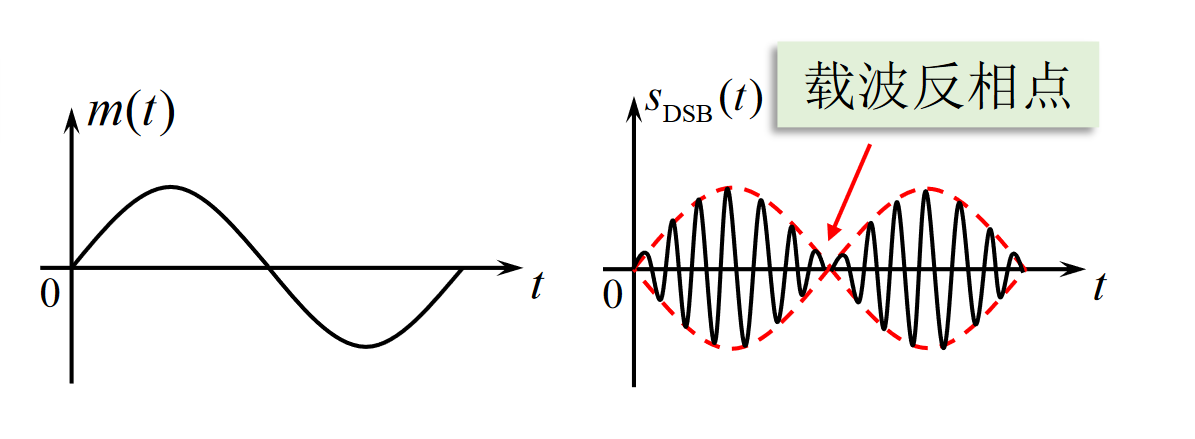
DSB信号时域波形图
DSB信号的包络与$m(t)$不成正比,在$m(t)$的过零点处,载波相位有180°的突变,即存在载波反相点。
-
-
DSB信号的频域表达式及频谱
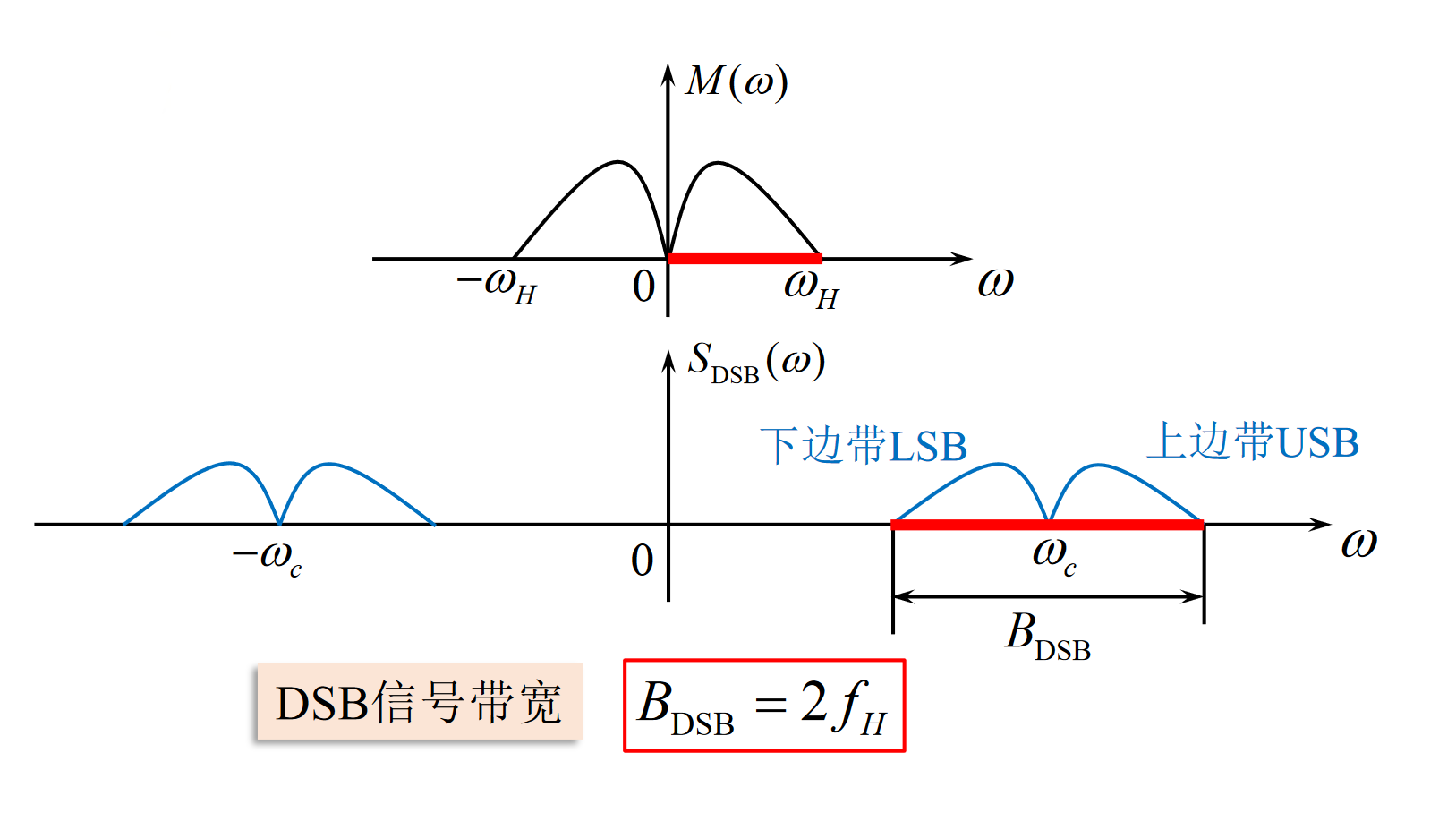
- 频域表达式:$$S_{\mathrm{DSB}}(\omega)=\frac12{\left[M(\omega+\omega_c)+M(\omega-\omega_c)\right]}$$
- DSB信号频域波形图
-
DSB信号调制效率
-
DSB信号的特点
- 包络与$m(t)$不成正比;
- 在$m(t)$的过零点处,载波相位有$180^o$的突变,即存在载波反相点;
- 已调信号带宽: $B_{DSB}=2f_H$
- 已调信号功率:$\begin{aligned}P_{\text{DSB}} = & \overline { m ^ 2 ( t ) }=P_S\end{aligned}$
- 功率利用率高,为100%
2.3 单边带调制SSB
-
SSB调制原理图(滤波法)
-
$H_{SSB}(w)$滤波特性
滤波法难点:要求边带滤波器在载频$w_c$,处具有陡峭的截止特性。由于理想滤波特性物理不可实现,实际中滤波器从通带到阻带存在过渡带,因此要求$m(t)$信号频谱在ω=0处近似为0。
-
SSB调制数学原理(相移法)
-
相移法原理框图
相移法难点:宽带相移网终设计困难,需要相干载波。
- SSB信号的特点
- 已调信号带宽:$B_{SSB}=f_H$
- 低功耗特性:无需传送载波和另一边带,功率利用率高,适用于频带拥挤的移动通信场景;
- 缺点:设备较复杂,滤波器设计存在技术难点,需要相干解调。
三.非线性调制:FM和PM
3.1 角度调制的基本概念



3.2 窄带调频(NBFM)
-
前提条件:FM信号的最大瞬时相位偏移满足 $\left|K_f\int m(\tau)\mathrm{d}\tau\right|\ll\frac\pi6\text{ (或0.5)}$
-
时域表达式和频谱表达式:
-
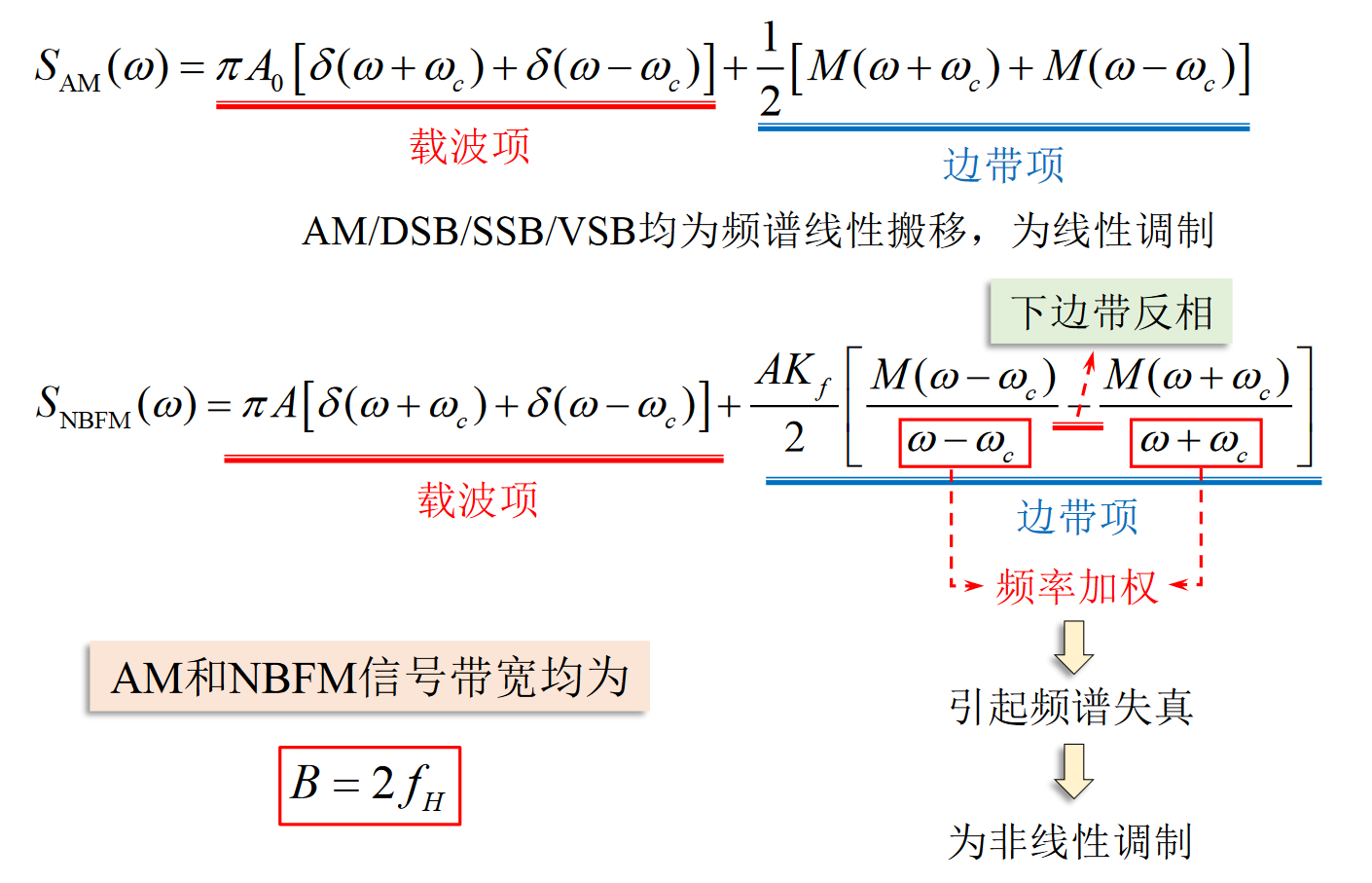
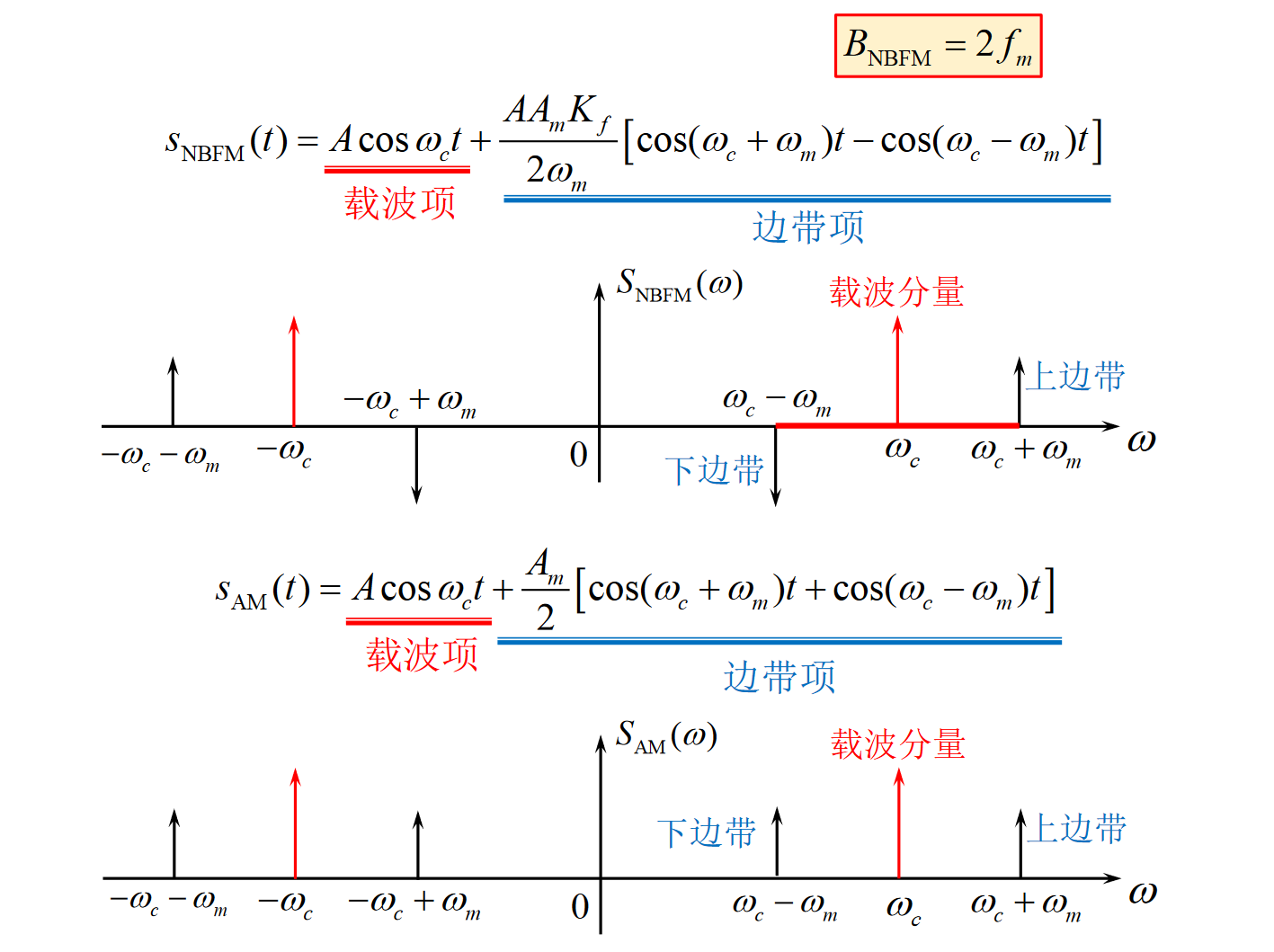
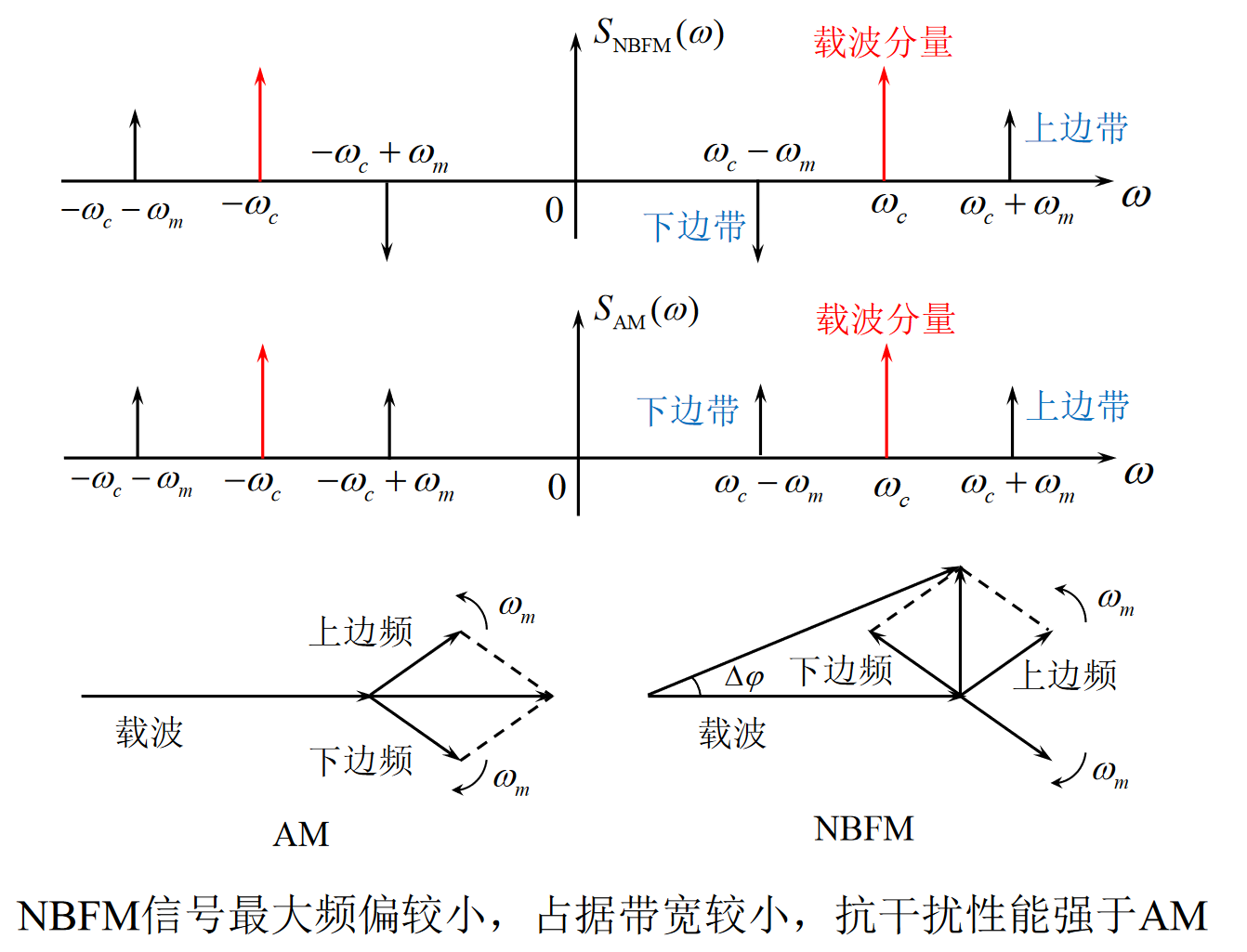
窄带调频信号和AM信号的比较
-
窄带调频信号和AM信号的比较
3.3 宽带调频
-
前提条件:FM信号的最大瞬时相位偏移不满足 $\left|K_f\int m(\tau)\mathrm{d}\tau\right|\ll\frac\pi6\text{ (或0.5)}$
-
宽带调频带宽及功率分配