🌈以下是本人对《通信原理》第四章 信道的学习，是为了方便后续的学习，如有补充和错误，欢迎评论区留言！相关参考资料和视频已放在文末。

一.信道的定义和分类

1.1 信道的定义

  • 狭义信道：信号的传输媒介
  • 广义媒介：调制器的输出到解调器的输入、编码器的输入到解码器的输出。

1.2 信道的分类

  1. 根据输入输出信号分类
  • 连续信号：调制信道
  • 离散信号：编码信道
  1. 根据信道的传输介质分类
  • 有线信道
  • 无线信道
  1. 根据信道的特性分类
  • 恒参信道
  • 随参信道

二.信道的数学模型

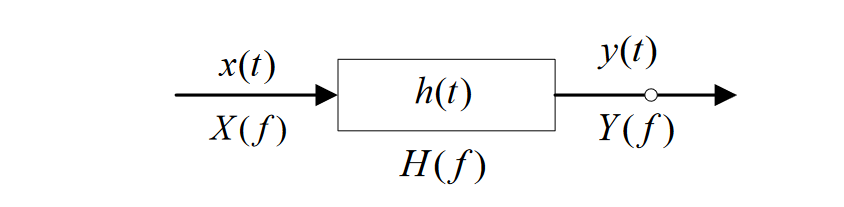
2.1 调制信道的数学模型

1711425565424.png
表达式：$e_{0}(t)=k(t)e(t)+n(t)$，其中$k(t)$为乘性干扰，$n(t)$为加性干扰。若$k(t)$变化缓慢或者不变化，那么该信道称为恒参信道，反之则称为随参信道。

2.2 编码信道的数学模型（二进制编码信道）

1711425983219.png
编码信道有关的概率计算：

  1. 转移概率：$P(0/0)=1-P(1/1)$ $P(1/1)=1-P(0/0)$
  2. 误码率：$P_e=P(0)P(1/0)+P(1)P(0/1)$
  3. Y的概率：$P(Y=0)=P(X=0)P(0\mid0)+P(X=1)P(0\mid1)$ $P(Y=1)=P(X=0)P(1\mid0)+P(X=1)P(1\mid1)$

三.信道特性及对传输信号的影响

3.1 恒参信道

  1. 传输特性
  • $H(w)=\left|H(w)\right|e^{j\varphi(w)}$
  • 幅频特性：$\left|H(w)\right|\sim\mathrm{W}$
  • 相频特性：$\varphi(\mathrm{w})\sim\mathrm{W}$
  1. 无失真传输
    1711426794509.png
  • 时域条件：$y(t)=Ax(t-t_{0})$，$h(t)=A\delta(t-t_0)$，其中A为一个幅度常量。
  • 频域条件：$H_{(w)}=Ae^{-jwt_0}$
  • 时延特性：$\tau(w)=-\frac{\varphi(w)}w$
  • 群时延特性：$\tau_G(w)=-\frac{d\varphi(w)}{dw}$
    注意：信号不失真的充要条件是，幅频特性为常数，时延特性为常数（非群时延。）

3.2 随参信道

  1. 三个特性
  • 第一：对信号的衰减随时间变化。
  • 第二：对信号的时延随时间变化。
  • 第三：多径传播。
  1. 多径传播
    指发射点出发的信号经过多条路径到达接收端。由于每条路径的时延和衰减都随时间而变化，所以接收信号是衰减和时延随时间变化的各路径信号的合成。
    $$R(t)=\sum_{i=1}^n\mu_i(t)\cos w_0[t-\tau_i(t)]=\sum_{i=1}^n\mu_i(t)\cos[w_0t+\varphi_i(t)]$$
    其中$\mu_i(t)$为第$i$条路径到达的接收信号的振幅；$\tau_i(t)$为第$i$条路径到达的接收信号的时延。
    相关带宽：$B=\frac1{\tau_m}$，（$\tau_m$为多径中最大的相对时延差）,当信号带宽大于相关带宽时，会产生严重的失真或者码间干扰。
    以两条路径传输信号说明多径传播：
    1711428221382.png

3.3 随参信道改善方法

  • 采用分集接收
  • 采用抗衰落的调制解调技术
  • 加大发射功率等

四.信道容量

4.1 定义

  • 定义一：单位时间内能够传输的平均信息量最大值。单位：bit/s
  • 定义二：每个符号能够传输的平均信息量最大值。单位：bit/Baud或bit/符号。

4.2 连续信道容量

  1. 香农公式
  • 定义：$C=B\log_2(1+\frac SN)$。$B为信道带宽。
    $$\frac{S}{N}=\frac{S}{n_{0}B}$$
  • 前提：信号服从高斯分布，噪声为高斯白噪声。
  • 结论：
    ①$C$随着$\frac SN$增大而增大。
    ②$\text{当}n_0\to0\text{时,}C\to\infty$，即无干扰信道的信道容量为无穷大。
    ③$C$随着$B$增大而增大，但不能无限增大，即：当$B\to\infty,C\to1.44\frac SN$
    ④当信道信息速率$R≤C$，则理论上可实现无差错传输，当$R>C$,则不能实现无差错传输。

4.3 离散信道容量

  1. 熵 （一个符号所含的平均信息量）
    $$H(Y)=-\sum_{j=1}^mP(y_j)\log P(y_j)$$
    特殊地，离散二进制熵函数，当为二进制信源时，设发送1的概率为$P(1)=a$，则发送"0"的概率$P(0)=1-a$,则信源的熵$H(a)$可表示为：
    $$H(a)=-a\log_2^a-(1-a)\log_2^{1-a}$$
  2. 条件熵
  • 定义：已知一个符号的条件下，另外一个符号的信息熵。
    $$H(X\mid Y)=-\sum_{i=1}^n\sum_{j=1}^mP(x_iy_j)\mathrm{log~}P(y_j\mid x_i)\quad\quad\quad H(Y\mid X)=-\sum_{i=1}^n\sum_{j=1}^mP(x_iy_j)\mathrm{log~}P(y_j\mid x_i)$$
  • 性质：条件熵小于等于其自身的信息熵。即$H(Y|X){\leq}H(Y)$，$H(X|Y){\leq}H(X)$

1711461213371.png