通信原理学习之路：第三章 随机过程

🌈以下是本人对《通信原理》第三章 随机过程的学习，是为了方便后续的学习，如有补充和错误，欢迎评论区留言！相关参考资料和视频已放在文末。

第三章 随机过程

一.通信原理中的概率论知识

1.1 随机变量

1. 离散型随机变量：所有的值都可以逐一列举出来，例如骰子的点数。概率用P表示。

• 非负性：$ \quad p_k{\geqslant}0\text{;} \quad k{=}1,2, . . .$
• 规范性：$ \quad \sum_{i=1}^{\infty}p_{i}=1$

2. 连续型随机变量：全部可能取值是无穷的，不能被逐一列举，如手机的使用寿命。其概率密度函数用f(x)或者p(x)表示。

概率密度函数：
  设X为一随机变量，若存在非负实函数f(x),使对任意实数a<b,有
$${P{(a\leq X<b)}=\int_a^bf(x)dx}$$
 则称X为连续型随机变量，f(x)称为X的概率密度函数，简称概率密度或密度函数.

• $ f(x)>0 $
• $ \int_{-\infty}^{\infty}f(x)dx = 1 $
• $ {P{(a\leq X<b)}=\int_a^bf(x)dx = F(a) - F(b)} $

1.2 期望

1. 离散型随机变量的数学期望
   定义：设离散型随机变量X的分布律为：

$X$	$X_{1}$	$X_{2}$	$X_{3}$	…	$X_{K}$
$P$	$P_{1}$	$P_{2}$	$P_{3}$	…	$P_{K}$

通常记数学期望为：$$E(X)=\sum_{k=1}^{\infty}x_{k}P_{k}$$
若存在随机变量 $ Y=g(x)，则$ $$E(Y)=\sum_{k=1}^{\infty}g(x_{k})P_{k}$$
2. 连续型随机变量的数学期望
定义：设连续型随机变量X的概率密度为f(x)。则X的期望为：
$$E(X)=\int_{-\infty}^{+\infty}xf(x)dx$$
定义：设X为连续型随机变量，其概率密度函数为$f_{X}(x)$，又随机变量$Y=g(x)$，当
$$\int_{-\infty}^{+\infty}\lvert g(x)\rvert f_X(x)dx \quad 收敛时有：E(Y)=E(g(x))=\int_{-\infty}^{+\infty}g(x) f_X(x)dx$$
3. 常见的连续型随机变量

• 正态分布
• 均匀分布
• 一般正态分布

若$X\sim N(0,1) 表示随机变量X 满足正态分布，其f_{X}(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^{2}}{2}}$
$$\int_{-\infty}^{+\infty}e^{-\frac{x^{2}}{2}}dx=\sqrt{2\pi}$$

若$X\sim u(a,b) 表示随机变量X在a到b上满足均匀分布，其随机变量X的概率密度为$
$$ a ≤ X ≤ b, f(x) = \frac{1}{b-a} $$
$$ E(X)=\frac{a+b}{2} \quad D(X)=\frac{1}{12}(b-a)^{2}$$

若$X\sim N(\mu,\sigma^2) 表示随机变量X 满足正态分布，其f_{X}(x) =\frac1{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$
$$E(X)=\mu \quad D(X)=\sigma^2$$

二.随机过程

2.1 随机过程的基本概念

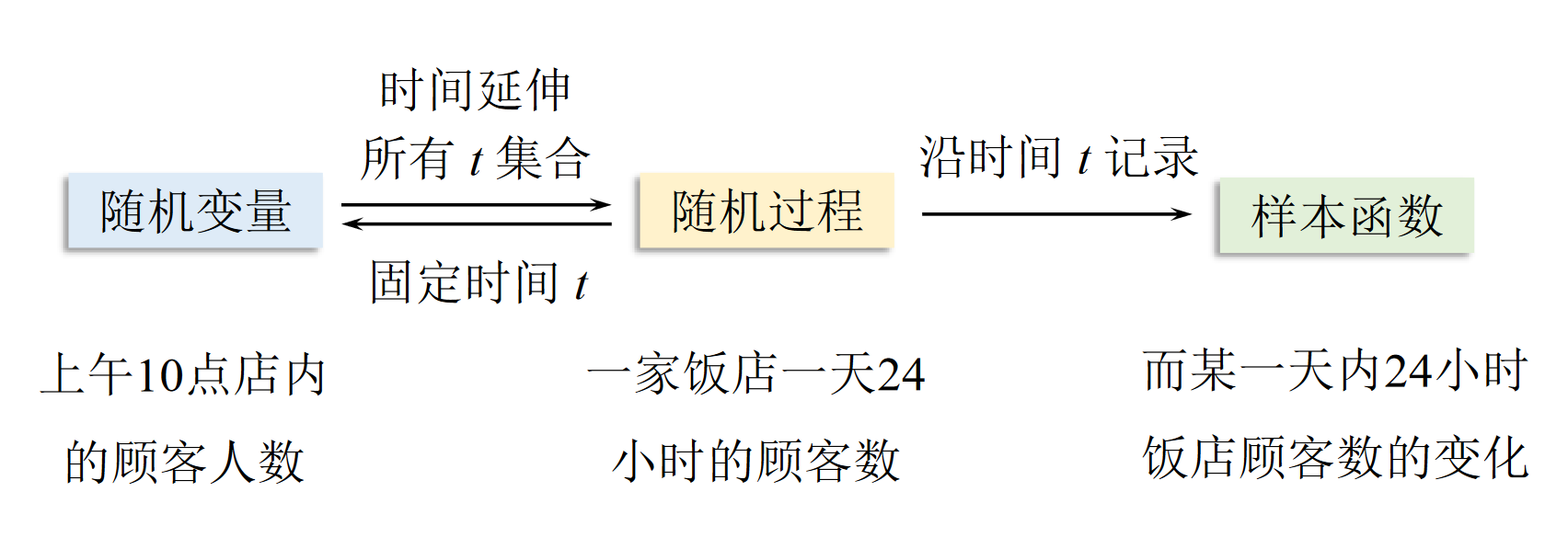
  随机过程${x(t)}$由一族时间函数$x_i(t),i=1,2,3,…$组成，每一个时间函数$x_i(t)$称为随机过程$x(t)$的一个样本函数。
  每个样本函数在时间上，在幅度取值上都是连续变化的波形。若固定时刻，随机过程在该时刻所有样本函数的取值则为一随机变量。
  为了描述随机过程在不同时刻的相互关系，用维联合分布函数(概率密度函数族)来描述n个不同时刻对应的n个随机变量。

2.2 随机过程统计特性

1. 一维分布函数与一维概率密度函数

• 一维分布函数
• 一维概率密度函数

$$F_1(x_1,t_1)=P[\xi(t_1)\leq x_1]$$
$$\begin{cases}0\leq F_1(x_1,t_1)\leq1\F_1(-\infty,t_1)=0,~F_1(+\infty,t_1)=1\x_2>x_1,~F_1(x_2,t_1)>F_1(x_1,t_1)\end{cases}$$

$$f_1(x_1,t_1)=\frac{\partial F_1(x_1,t_1)}{\partial x_1}$$
$$\begin{cases}f_1(x_1,t_1)\geq0\F_1(x_1,t_1)=\int_{-\infty}^{x_1}f_1(x_1^{\prime},t_1)\mathrm{d}x_1^{\prime}\P[a_1\leq\xi(t_1)\leq a_1]=\int_{a_1}^{a_2}f_1(x_1,t_1)\mathrm{d}x_1\\int_{-\infty}^{+\infty}f_1(x_1,t_1)\mathrm{d}x_1=1&\end{cases}$$

2. n维分布函数与n维概率密度函数
   $$F_n(x_1,x_2,\cdots,x_n;t_1,t_2,\cdots,t_n)=P[\xi(t_1)\leq x_1,\xi(t_2)\leq x_2,\cdots,\xi(t_n)\leq x_n]$$
   $$f_n(x_1,x_2,\cdots,x_n;t_1,t_2,\cdots,t_n)=\frac{\partial F_n(x_1,x_2,\cdots,x_n;t_1,t_2,\cdots,t_n)}{\partial x_1\partial x_2\cdots\partial x_n}$$

3. 数学期望
   $$a(t)=E\left[\xi(t)\right]=\int_{-\infty}^{+\infty}xf_1(x,t)\mathrm{d}x$$
   随机过程的数学期望与 t 有关，表示 n 个样本函数曲线的摆动中心。
   关于随机变量数学期望的一些性质：

• $E[C]{=}C\text{ 常数的数学期望是常数本身};$
• $E\left[aX_1+bX_2\right]=aE\left[X_1\right]+bE\left[X_2\right]$
• 对于两个统计独立的随机变量$$X_1,X_2\text{,有}E\begin{bmatrix}X_1X_2\end{bmatrix}=E\begin{bmatrix}X_1\end{bmatrix}E\begin{bmatrix}X_2\end{bmatrix}$$

4. 方差（方差 = 平方的期望 - 期望的平方）
   $$D[\xi(t)]=E\left{\left[\xi(t)-\alpha(t)\right]^2\right}=E\left[\xi^2(t)\right]-a^2(t)$$
   随机过程的方差表示了随机过程$\xi(t)$在 t 时刻偏离数学期望的程度。
   关于随机变量数学期望的一些性质：

• $D[C]{=}0\quad\text{常数的方差是}0;$
• $D[CX]{=}C^2D[X],D[X+C]{=}D[X]$
• $\text{对于两个不相关随机变量 }X_1,X_2\text{,有}$
  $$D\left[aX_1+bX_2\right]=a^2D{\left[X_1\right]}+b^2D{\left[X_2\right]}$$

5. 自相关函数和自协方差函数
   数学期望和方差只能反映随机变量$\xi(t)$在孤立时刻的数字特征，不能反映不同时刻的内在联系。

• 自相关函数
• 自协方差函数
• 两者关系

$$R(t_1,t_2)=E\left[\xi(t_1)\xi(t_2)\right]=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}x_1x_2f_2(x_1,x_2;t_1,t_2)\mathrm{d}x_1\mathrm{d}x_2$$
自相关函数反映不同时刻随机过程取值的相关性。

$$\begin{aligned}
B(t_1,t_2)& =E\left{\left[\xi(t_1)-a(t_1)\right]\left[\xi(t_2)-a(t_2)\right]\right} \
&=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}[x_1-a(t_1)][x_2-a(t_2)]f_2(x_1,x_2;t_1,t_2)\mathrm{d}x_1\mathrm{d}x_2
\end{aligned}$$
自协方差函数反映不同时刻随机过程的统计相关性。

$$B(t_1,t_2)=R(t_1,t_2)-a(t_1)a(t_2)$$
对于零均值随机过程：$B(t_1,t_2)=R(t_1,t_2)$
$\text{假定 }t_2>t_1\text{,令 }t_2=t_1+\tau\text{,则 }R(t_1,t_2)=R(t_1,t_1+\tau)\text{ ;}$
我们一般研究时间间隔$\tau$对相关性的影响；一般情况下，$\tau$越大，相关性越小。

6. 互相关函数和互协方差函数

• $$R_{\xi\eta}(t_1,t_2)=E\left[\xi(t_1)\eta(t_2)\right]$$
• $$B_{\xi\eta}(t_1,t_2)=E\left{\left[\xi(t_1)-a_\xi(t_1)\right]{\left[\eta(t_2)-a_\eta(t_2)\right]}\right}$$

三.平稳随机过程

3.1 平稳随机过程的定义

平稳随机过程的统计特性不随时间的推移而变化，其一维分布与时间 t 无关，二维分布只与时间间隔$\tau$有关。即：
$$f_1(x,t)=f_1(x,t+h)=f_1(x)\quad\forall h$$
$$\begin{aligned}
f_2(x_1,x_2;t_1,t_2)& \begin{aligned}=f_2(x_1,x_2;t_1+h,t_2+h)\end{aligned} \
&=f_2(x_1,x_2;t_2-t_1)=f_2(x_1,x_2;\tau)\quad\forall h
\end{aligned}$$

3.2 平稳随机过程的数字特征

• 均值：$E\left[\xi(t)\right]=\int_{-\infty}^{+\infty}xf_1(x)\mathrm{d}x=a$，与t无关，样本函数围绕一水平线起伏。
• 方差：$D[\xi(t)]=\int_{-\infty}^{+\infty}(x-\alpha)^2f_1(x)\mathrm{d}x=E{\left[\xi^2(t)\right]}-\alpha^2=\sigma^2$，与t无关，为常数。
• 自相关函数：
  $$\begin{aligned}
  R(t,t+\tau)& =E\left[\xi(t)\xi(t+\tau)\right] \
  &=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}x_1x_2f_2(x_1,x_2;\tau)\mathrm{d}x_1\mathrm{d}x_2=R(\tau)
  \end{aligned}$$
  自相关只与时间间隔$\tau$有关，而与时间起点无关。

3.3 狭义（严）平稳和广义（宽）平稳

一个二阶矩随机过程，均值为常数，自相关函数仅仅是时间间隔的函数，称这样的过程为广义平稳随机过程或宽平稳随机过程。

1. 平稳随机过程的各态历经性
   假定$x(t)$为随机过程$\xi (t)$的任意一个实现，其时间均值和时间相关函数分别为：
   $$\overline{a}=\overline{x(t)}=\lim_{T\to\infty}\frac1T\int_{-T/2}^{T/2}x(t)\mathrm{d}t\quad\overline{R(\tau)}=\overline{x(t)x(t+\tau)}=\lim_{T\to\infty}\frac1T\int_{-T/2}^{T/2}x(t)x(t+\tau)\mathrm{d}t$$
   若平稳随机过程依概率满足：$\overline{a}=a,\overline{R(\tau)}=R(\tau)$，则称该平稳过程具有各态历经性。

2. 平稳随机过程自相关函数性质

• $R(0)=E\left[\xi^2(t)\right]=S\quad$物理意义：随机过程的平均功率；
• $R(\infty)=E^2\left[\xi(t)\right]=\alpha^2$ 物理意义：随机过程的直流功率； 时间间隔无限大时，$\xi(t)$与 $\xi(t+\tau)$趋于独立，由于平稳，$E\left[\xi(t+\tau)\right]=E\left[\xi(t)\right]$
  $$R(\infty)=\lim_{\tau\to\infty}E\left[\xi(t)\xi(t+\tau)\right]=\lim_{\tau\to\infty}E\left[\xi(t)\right]E\left[\xi(t+\tau)\right]=E\left[\xi(t)\right]E\left[\xi(t)\right]=E^2\left[\xi(t)\right]$$
• $R(0)-R(\infty)=E\left\lfloor\xi^2(t)\right\rfloor-\alpha^2=\sigma^2$ 物理意义：随机过程的交流功率；
  $$
  \text{对应方差公式 }D{\left[\xi(t)\right]}=E{\left[\xi^2(t)\right]}{-}E^2{\left[\xi(t)\right]}
  $$
• $R(\tau)=R(-\tau)$ 自相关函数为偶函数；
• $\begin{vmatrix}R(\tau)\end{vmatrix}\leq R(0) $给出了自相关函数的上界，与白身时刻相关性最大。

3.4 平稳随机过程的功率谱密度

1. 定义
   假定 $f(t)$为随机过程 $\xi(t)$的任一实现，对其进行 $T$ 长度的截断，记为$f_T(t)$, 其傅里叶变换为$F_T(\omega)$,则任一实现的功率谱为：
   $$P_f(\omega)=\lim_{T\to\infty}\frac{\left|F_T(\omega)\right|^2}T$$
   $\text{故 }\xi(t)\text{ 的功率谱密度为}\mathbf{:}$
   $$\begin{aligned}P_\xi(\omega)=E\Big[P_f(\omega)\Big]=\lim_{T\to\infty}\frac{E\Big[\Big|F_T(\omega)\Big|^2\Big]}{T}\end{aligned}$$

2. 维纳-辛钦定理
   平稳随机过程 $\xi(t)$的功率谱密度函数$P_{\varepsilon}(\omega)$和自相关函数 $R(\tau)$ 为一对傅里叶变换对。
   $$\begin{cases}P_{\xi}(\omega)=\int_{-\omega}^{+\infty}R(\tau)e^{-j\omega\tau}\mathrm{d}\tau\R(\tau)=\frac1{2\pi}\int_{-\omega}^{+\infty}P_{\xi}(\omega)e^{j\omega\tau}\mathrm{d}\omega&\end{cases}\text{或}\quad\begin{cases}P_{\xi}(f)=\int_{-\infty}^{+\infty}R(\tau)e^{-j2\pi f\tau}\mathrm{d}\tau\R(\tau)=\int_{-\infty}^{+\infty}P_{\xi}(f)e^{j2\pi f\tau}\mathrm{d}f&\end{cases}\color{red}{R(\tau)}\Longleftrightarrow P_{\xi}(f)$$

3. 功率谱密度的性质

• $$\text{功率谱密度具有非负性:}\quad P_\xi(f){\geq}0$$
• $$\text{功率谱密度是偶函数:}P_\xi(-f)=P_\xi(f)$$
• 单边、双边功率谱密度互换：$$P_{\xi^\text{单边}}(f)=\begin{cases}2P_{\xi^\text{双边}}(f)&f\geq0\0&f<0&\end{cases}$$

4. 平均功率计算方法
   $$S=R(0)=E\left[\xi^2(t)\right]\quad\quad S=\int_{-\infty}^{+\infty}P_\xi(f)\mathrm{d}f=\frac1{2\pi}\int_{-\infty}^{+\infty}P_\xi(\omega)\mathrm{d}\omega $$